Зная закон движения и массу точки, определить силу, действующую на точку

Первая и вторая задачи динамики.

Первая (прямая) задача.

Для решения этой задачи необходимо знать ускорение точ­ки.

1. Пусть движение точки задано в декартовых координатах

, ,

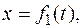
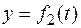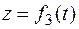Определяем проекции ускорения на оси координат

,

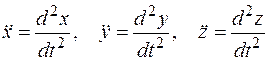а затем - проекции 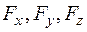силы на эти оси:

.

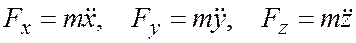Модуль и направление силы определяется по формулам

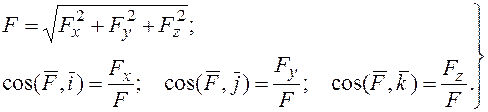
2. Если точка совершает криволинейное движение и извес­тен закон движения 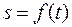, траектория точки и ее радиус кри­визны 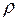, то удобно пользоваться естественными осями, а про­екции ускорения на эти оси определяются по фор­мулам:

на касательную ось

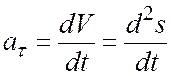— касательное ускорение,

на нормаль

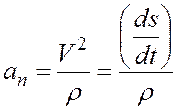— нормальное ускорение.

Проекция ускорения на бинормаль равна нулю. Тогда проекции силы на естественные оси

.

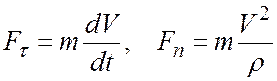Модуль и направление силы определяется по формулам:

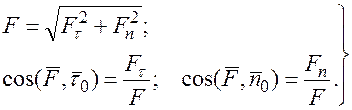
Задача 1. Автомобиль массы т = 1000 кг движется по выпуклому мосту со скоростью V = 20 м/с. Радиус кривизны в середине моста 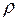= 100 м. Определить силу давления автомобиля на мост в момент, когда он находится на середине моста.

Решение. Считая автомобиль материальной точкой, изобразим его в середине моста и покажем силы: вес 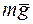и нормаль­ную реакцию .

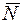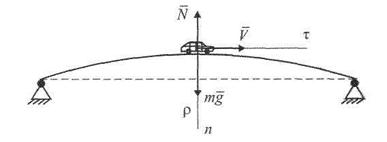
Второй закон динамики в векторной форме

.

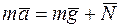Спроецируем это равенство на естественные ос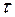и и :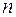

,

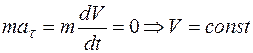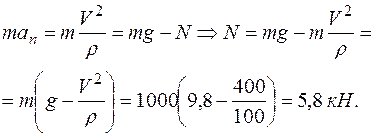
Задача 2. В кабине лифта, движущегося вверх рав­ноускоренно без начальной скорости, стоит человек массы т. Определить давление че­ловека на пол кабины, если за время t ка­бина поднялась на высоту h.

Решение. Объект движения — человек. Ось Ох направим в сторону движения. На человека действует реакция пола 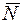и его вес .

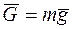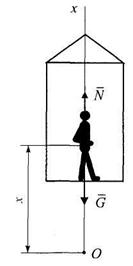
Запишем второй закон динамики в век­торной форме и затем в проекции на ось х:

.

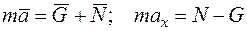Проекция ускорения на ось х

/

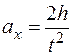Реакция пола

.

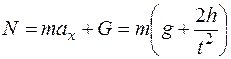Давление человека на пол равно реакции N и направлено в противоположную сторону.

При движении лифта вниз ось х на­правляется также вниз. Тогда

,

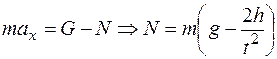т. е. давление в этом случае меньше силы тяжести.

Вторая (обратная) задача.

Дата добавления: 2014-01-03