И параметрически

2.1. Дифференцирование функций заданных неявно

Пусть зависимость между аргументом и функцией задана уравнением 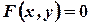, т.е. уравнение не разрешено явно относительно переменной .

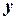О.2.1.Функция, заданная уравнением

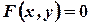(2)

называется заданной неявно, если оно обращается в тождество при замене 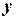на 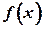на некотором промежутке 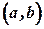, т.е.

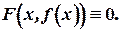
Считаем, что условия существования и дифференцируемости неявной функции выполнены (теорема будет сформулирована в теме «Функции нескольких переменных») т.е. уравнение (2) определяет некоторую функцию.

Например: 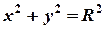- уравнение окружности определяет функцию 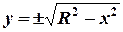, которая будучи подставленной в уравнение приведет его к тождеству. Однако это возможно не всегда.

Правило дифференцирования неявной функции.

Для нахождения производной функции, заданной неявно, нужно продифференцировать уравнение (2) помня, что 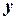является функцией от 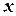и его производная равна 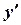. Затем разрешить полученное уравнение относительно .

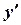Производная неявной функции сама является функцией неявной.

Замечание 2. Термины «явная функция», «неявная функция» характеризуют не способы задания функции, а характер зависимости 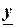от 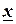. Каждая явная функция 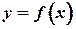, может быть представлена как неявная:

.

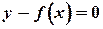Пример. Найти производную функции

.

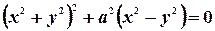Решение.

Функция задана неявно. Дифференцируем данное уравнение по 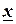помня, что 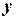есть функция от 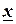, т.е. 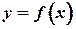, получим:

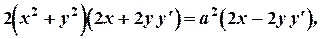
откуда

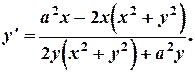
2.2. Дифференцирование функций заданных параметрически

В геометрии при изучении линий на плоскости и в пространстве мы познакомились с их параметрическими уравнениями. Параметрическое задание кривых широко применяется в механике. Если в плоскости движется некоторая материальная точка и известны законы движения проекций этой точки на оси координат

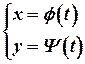(3)

где параметр 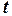есть время, то уравнение (3) есть параметрическое уравнение траектории движущейся точки. Исключая из (3) параметр 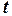, получим уравнение траектории в форме 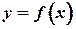(в явном виде) или 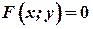(в неявном виде).

О.2.2. Функция 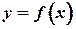называется заданной параметрически, если и аргумент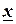 и функция 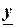есть функции одной и той же вспомогательной переменной - параметра .

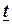((3) - параметрическое задание функции ).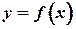

Отыскание из системы (3) непосредственной связи между 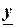и 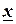без участия переменной 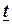называется исключением параметра.

Итак, пусть функция 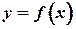задана параметрически системой (3), где .

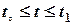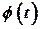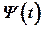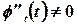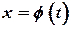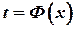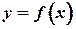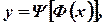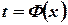Предположим, что функции и дифференцируемы и функция имеет обратную , которая также дифференцируема. Тогда заданную параметрически функцию можно рассматривать как сложную функцию где , а 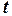- промежуточный аргумент.

По правилу дифференцирования сложной функции получим:

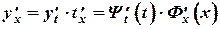(4)

На основании теоремы о дифференцировании обратной функции

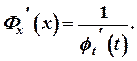
Подставляя 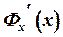в равенство (4), получим

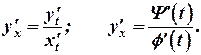(5)

Полученная формула (5) дает возможность находить производную 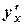параметрически заданной функции не исключая параметра.

Пример. Функция задана параметрически уравнениями:

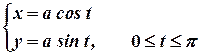
Найти .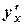

Решение

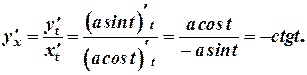
Дата добавления: 2014-01-03