ПРОВЕРКА ПАРАМЕТРИЧЕСКИХ ГИПОТЕЗ

12 3 Следующая ⇒

Параметрические гипотезы несут в себе суждения о параметрах распределения. Как уже отмечалось, параметры распределения зачастую связаны с числовыми характеристиками, поэтому для нормального закона проверка гипотез о параметрах распределения сводится к проверке гипотез о числовых характеристиках.

Предположим, что изучаемая случайная величина распределена по нормальному закону с параметрами m=E[ξ] и s²=V[ξ].

В том случае, когда оба параметра распределения неизвестны, вычисляют их оценки: оценку 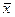неизвестного математического ожидания и S² - оценку дисперсии. Для проверки сформулированной гипотезы вычисляют выборочную статистику по формуле:

· .

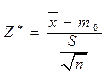Если основная гипотеза Н₀верна, то указанная случайная величина Z* распределена по закону Стьюдента с (n-1) степенью свободы. При указанной альтернативной гипотезе критическая область является двусторонней. Поэтому по таблицам распределения Стьюдента по заданному уровню значимости 1-α и n-1 степени свободы ищут симметричную критическую точку распределения t_1-α=к₂, к₁=-к₂ . В том случае, когда | Z^*| < к₂, принимают основную гипотезу. Если же | Z^*| ≥ к₂,то принимают альтернативную гипотезу, основную отклоняют.

Следует иметь в виду, что когда альтернативная гипотеза Н_а имеет вид:

Н_а: m > m₀

12 3 Следующая ⇒

Дата добавления: 2014-01-03; Просмотров: 1143; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

ПОИСК ПО САЙТУ: