Гипотезы об однородности двух выборок

Или

H_a: m < m_{0 ,}

критические области будут соответственно право и левосторонними. Поэтому границу области ищут по таблицам распределения Стьюдента, в которых указано «односторонняя». В первом случае принимают основную гипотезу, если Z^*<к₂, во втором случае принимают основную гипотезу, если Z^*>к₁.

Отметим также, что проверку основной гипотезы можно проводить, используя следующую выборочную статистику:

,

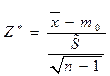если для оценивания дисперсии использовалась смещенная оценка.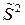

В Stata проверку гипотезы о величине математического ожидания можно проводить следующим образом:

1. Используя стандартные программы из меню Statistics. Например, в данном случае

one sample mean – comparison test

2. Используя команду, которую записываем в командной строке

ttest Var1=m0

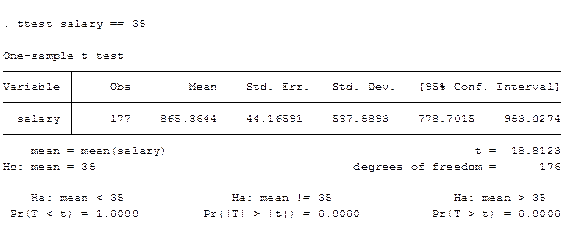
Для второго параметра – дисперсии, формулируют следующие основную и альтернативную гипотезы:

H₀: s²=s²₀,

H_a: s²¹s²₀ .

Проверка основной гипотезы основана на теореме о том, что если основная гипотеза верна, то следующая выборочная статистика

·

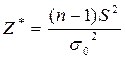
распределена по закону χ² с (n-1) степенью свободы. Критическая область будет являться двусторонней, ее границы к₁ и к₂ ищут из условия:

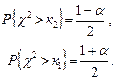
по таблицам критических точек распределения χ² (Приложение 5).

Если выборочная статистика Z* удовлетворяет неравенству:

к₁<Z^*<к₂,

топринимают основную гипотезу, в противном случае принимают альтернативную гипотезу.

В том случае, когда альтернативная гипотеза формулируется следующим образом:

H_a: s²>s²₀

или так:

H_a: s²<s²₀,

критическая область будет соответственно право и левосторонней. В первом случае границу критической области ищут по соответствующим таблицам для критических точек χ² по заданному уровню значимости и (n-1) степени свободы из условия: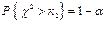. Во втором случае границу критической области ищут по соответствующим таблицам для квантилей χ² по заданному уровню значимости и (n-1) степени свободы из условия: .

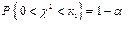Отметим также, что если для оценивания дисперсии использовалась смещенная оценка 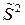, то проверку гипотезы о величине неизвестной дисперсии можно проводить, используя следующую выборочную статистику:

.

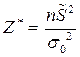В Стате для проверки гипотезы о величине дисперсии можно использовать следующую процедуру

one sample variance – comparison test

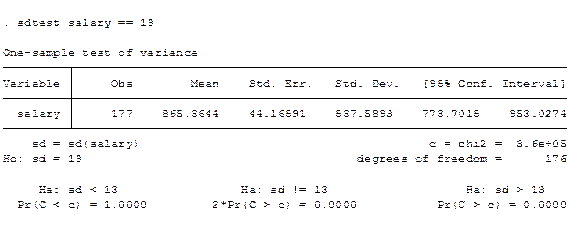
Или следующую команду:

sdtest salary=13

Рассмотрим теперь ситуацию, когда изучаются две нормально распределенные случайные величины: ξ₁ и ξ₂. Обозначим неизвестные параметры распределения первой случайной величиныm₁ и s₁ ( m₁=E[ξ₁], s₁²=V[ξ₁]), апараметры распределения второй случайной величиныm₂ и s₂ ( m₂=E[ξ₂], s₂²=V[ξ₂]). Предположим, что имеются выборки значений этих случайных величин объемов n₁ и n₂ соответственно. Рассмотрим как проводят проверку гипотез о равенстве параметров этих случайных величин. На первом этапе для каждой случайной величины по имеющимся выборкам объемов n₁ и n₂ соответственно, вычисляют выборочные средние и выборочные дисперси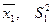и:и 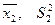, анализируют полученные результаты и выдвигают гипотезы:

H₀: m₁=m₂,

H_a: m₁¹m₂,

а затем следующие гипотезы:

H₀: s₁²=s²₂,

H_a: s₁²¹s²₂.

Для проверки первой группы гипотез о равенстве математических ожиданий

H₀: m₁=m₂,

H_a: m₁¹m₂,

вычисляют выборочную статистику вида:

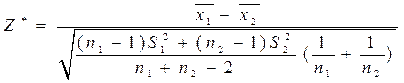
При справедливости основной гипотезы о равенстве математических ожиданий эта случайная величина Z* будет иметь распределение Стьюдента с (n₁+n₂-2) степенью свободы. Критическая область, при сформулированной альтернативной гипотезе, будет двусторонней. Ее границы ищут по таблицам критических точек распределения Стьюдента (двусторонних) по заданному уровню значимости (1-α) и (n₁+n₂-2) числу степеней свободы.Если выборочная статистика удовлетворяет неравенству к₁<Z^*<к₂, то принимают основную гипотезу о равенстве математических ожиданий. Если неравенство не выполняется, то принимают альтернативную гипотезу о том, что они не равны.

В том случае, если для дисперсий рассматриваемых случайных величин были вычислены смещенные оценки дисперсий 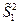, , 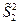то выборочную статистику для проверки гипотезы о равенстве математических ожиданий вычисляют по следующей формуле:

· .

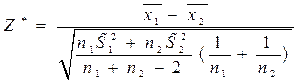Чтобы проверить гипотезу о равенстве дисперсий

H₀: s₁²=s²₂,

H_a: s₁²¹s²₂.

вычисляют следующую вспомогательную случайную величину:

· ,

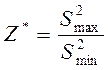где через S²_max обозначена большая из выборочных дисперсий S₁² и S₂², а через S_min²- меньшая.

Если основная гипотеза о равенстве дисперсий справедлива, то вспомогательная случайная величина Z^* распределена по закону Фишера с (n_max - 1, n_min - 1) степенями свободы. Критическая область будет правосторонней, ее границу ищут по таблицам распределения Фишера по уровню значимости (1-α)/2 и (n_max - 1, n_min -1) степеням свободы. Если выполняется неравенство: 0 <Z^*<к₂, то принимают основную гипотезу о равенстве дисперсий,если выполняется неравенство Z^* ≥ к₂, то основную гипотезу отклоняют в пользу альтернативной.

В тех случаях, когда альтернативная гипотеза будет иметь вид:

H_a: s₁²> s²₂.

выборочная статистика вычисляется по такому же правилу, а границу критической области к₂ ищут уже по уровню значимости (1-a) и (n_мах-1, n_мин-1) степеням свободы.

В Стате для сравнения средних в случае независимых выборок (два случая, в предположении, что дисперсии равны и в предположении, что дисперсии не равны) используем:

two sample mean – comparison test

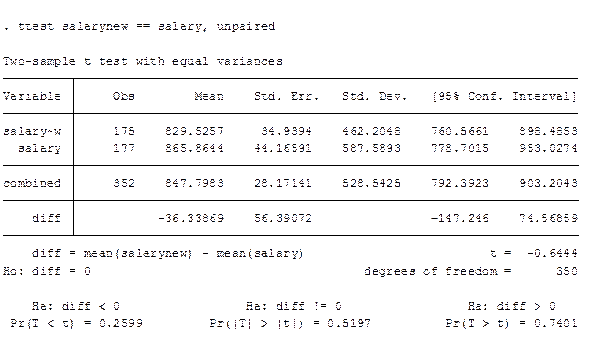
В Стате есть тест и для зависимых выборок:

В Стате:

two sample variance – comparison test

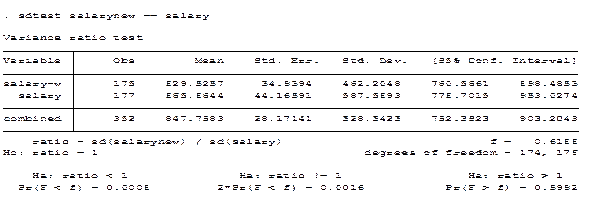
Дата добавления: 2014-01-03