Анализ корреляционной зависимости

Из теории вероятностей известно следующее свойство коэффициента корреляции 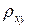: коэффициент корреляции 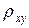двух случайных величин равен 1 или -1 тогда и только тогда, когда случайные величины связаны между собой линейно, т.е. у = ах + в.

Следует иметь в виду, что мы используем выборочный коэффициент корреляции. Эта характеристика является по своей сути случайной величиной и нельзя по ее значению делать категоричные выводы, подобные тем, которые производят, ориентируясь на 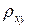. Все суждения, должны носить уже в этом случае более осторожный, вероятностный характер.

На сегодняшней лекции рассмотрим методы тестирования гипотезы о некоррелируемости двух случайных величин. Это позволит нам использовать выборочный коэффициент корреляции для оценки тесноты связи между двумя случайными величинами. Отметим еще раз, что коэффициент корреляции Пирсона, который мы изучаем в данном курсе применяется для анализа корреляционной зависимости между переменными, измеренными в метрической шкале. Для анализа корреляционной зависимости порядковых переменных используют коэффициент (ранговой) корреляции Спирмена, а для переменных, измеренных в номинальной шкале используют коэффициент Фи.

Корреляционный анализ между двумя случайными величинами проведем следующим образом: вычислим все выборочные числовые характеристики x и y и, самое главное, вычислим .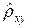

Выдвинем основную гипотезу H₀ о том, что переменные x и y некоррелированные:

H₀: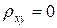

и альтернативную гипотезу H_а:

H_а: .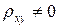

Дата добавления: 2014-01-03