Правило сложения дисперсий, межгрупповая дисперсия

В общем случае вариация результативного признака обусловлена различными факторами в их совокупности, а не только воздействием одного из них. Если статистическую совокупность разбить на группы по какому-либо признаку, то наряду с изучением вариации результативного признака по всей совокупности в целом под воздействием всех факторов получаем возможность изучить вариацию для каждой из составляющих всю совокупность групп по отдельности. Также можно изучить при этом вариацию между группами. В простейшем случае вся исходная совокупность разбивается на отдельные группы по одному фактору. Тогда указанный выше анализ вариации сводится к расчету и анализу трех видов дисперсии: общей, внутригрупповой и межгрупповой.

Общая дисперсия измеряет вариацию результативного признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперсия δ ² характеризует систематическую вариацию под воздействием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней для всей совокупности:

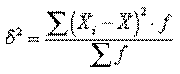, (12)

где f — численность единиц в группе (частота).

Внутригрупповая дисперсия есть уже известная нам дисперсия (для всей совокупности, называемая общей), но теперь эта формула применяется только к отдельной группе. Соответственно и обозначается она σ², но уже с индексом i, который подчеркивает, что расчет выполняется для отдельной i -группы.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. ту ее часть, которая обусловлена влиянием прочих (неучтенных) факторов, отличных от основания группировки. По отдельным внутригрупповым дисперсиям, рассматривая их как значения некоторого особого признака, рассчитывают среднюю по внутригрупповым дисперсиям, которая уже характеризует вариацию по всей совокупности в целом под воздействием всех прочих (неучтенных) факторов, отличных от основания группировки.

Существует простая и важная формула, связывающая общую дисперсию, межгрупповую дисперсию и среднюю по внутригрупповым дисперсиям:

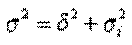. (13)

Это означает, что общая дисперсия равна сумме межгрупповой дисперсии и средней по внутригрупповым дисперсиям. Следовательно, зная две из трех дисперсий, можно всегда найти и третью.

Правило сложения дисперсий показывает, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый результативный признак. Такие соображения естественным образом приводят к количественной характеристике такого влияния, мере стохастической связи между признаками. Она называется эмпирическим коэффициентом детерминации и обозначается η ², характеризуя силу влияния группировочного признака на образование общей вариации:

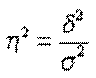. (14)

При отсутствии связи он просто равен нулю, при чисто функциональной связи — 1. В общем случае коэффициент детерминации принимает значения между 0 и 1. Это видно и из правила сложения дисперсий.

Помимо коэффициента детерминации используют также и эмпирическое корреляционное отношение, которое представляет собой корень квадратный из коэффициента детерминации. И опять оно весьма подходит для измерения линейной связи.

В общем случае нелинейной связи предпочтительнее использовать, что правильнее, коэффициент детерминации. Если связь отсутствует, то корреляционное отношение равно нулю и, следовательно, все групповые средние равны между собой, а межгрупповой вариации просто в этом случае нет.

Группировочный признак при этом никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение равно 1. Дисперсия групповых средних равна общей дисперсии и межгрупповой дисперсии, поэтому внутригрупповой вариации не будет. Таким образом, группировочный признак целиком определяет вариацию изучаемого результативного признака.

Определим среднее линейное, среднее квадратическое отклонение и дисперсию для нашего условного примера о распределении жите­лей города по величине месячного среднедушевого дохода. Все про­межуточные вычисления приведены в табл. 2.

Среднедушевой доход в среднем за месяц, тыс.руб	Число жителей в % к итогу (fi)	Середина интервала (xi)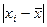
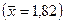
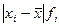
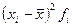
До 0,5	0,9	0,25	1,57	1,413	2,218
0,5 – 1,0	16,5	0,75	1,07	17,655	18,891
1,0 – 1,5	24,6	1,25	0,57	14,022	7,993
1,5 – 2,0	18,8	1,75	0,07	1,316	0,092
2,0 – 2,5	15,4	2,25	0,43	6,622	2,847
2,5 – 3,0	12,5	2,75	0,93	11,625	10,811
3,0 и более	11,3	3,25	1,43	16,159	23,107
Итого		-	-	68,812	65,959

Среднее линейное отклонение, дисперсия и среднее квадратическое отклонение соответственно составят:

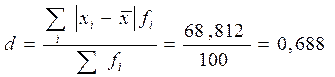тыс.руб.

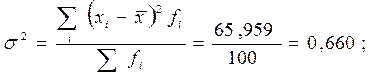
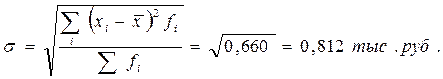
Среднее линейное и среднее квадратическое отклонения показы­вают, на сколько в среднем величина месячного среднедушевого до­хода жителей города отличалась от среднего дохода по городу. По формуле среднего линейного отклонения это отличие составляло: +- 688 руб., по формуле среднего квадратического отклонения: +-812 руб.

Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения.

Соотношение σ: d зависит от наличия в совокупности резких от­клонений и может служить индикатором «засоренности» совокупности нетипичными. выделяющимися из основной массы единицами. Для нормального распределения это соотношение равно 1,25.

Для оценки интенсивности вариации, а также для сравнения ее ве­личины в разных совокупностях или по разным признакам использу­ют относительные показатели вариации, которые рассчитываются как отношение абсолютных показателей вариации к средней величине признака: относительный размах вариации (коэффициент осцилля­ции); относительное линейное отклонение и др.

Наиболее часто на практике применяют коэффициент вариации (v), который представляет собой относительное квадратическое откло­нение:

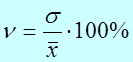(15)

По величине коэффициента вариации можно судить об интенсив­ности вариации признака, а следовательно, и об однородности соста­ва изучаемой совокупности. Чем больше величина коэффициента ва­риации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Существует шкала определе­ния степени однородности совокупности в зависимости от значений коэффициента вариации.

Коэффициент вариации (%)	Степень однородности совокупности
До 30	Однородная
30-60	Средняя
60 и более	Неоднородная

Отметим, что приведенная выше шкала оценки однородности со­вокупности весьма условна. Вопрос о степени интенсивности вариа­ции должен решаться для каждого изучаемого признака индивидуаль­но исходя из сравнения наблюдаемой вариации с некоторой ее обыч­ной интенсивностью, принимаемой за норму.

Для нашего примера коэффициент вариации составил:

,

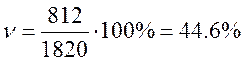что свидетельствует о средней колеблемости признака и, следователь­но, о средней однородности совокупности жителей города по величи­не среднедушевых доходов.

Вывод по 2-му вопросу: информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные по одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени.

Показатели вариации также являются составной частью или основой для расчетов других статистических показателей. Они используются в анализе взаимосвязей между признаками, в измерении структурных сдвигов в экономике, в оценке рисков.

Выводы по лекции: рассматривая зарегистрированные в процессе статистического наблюдения величины того или иного признака у отдельных единиц совокупности, можно обнаружить между ними различия. Колеблемость, многообразие, изменяемость величины признака у единиц совокупности называются вариацией.

Вариация порождается комплексом условий, действующих на совокупность и её единицы.

Исследование вариации в статистике имеет важное значение. Особенно актуально оно в настоящее время, когда формируется многоукладная экономика.

Измерение вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков, установить, например, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность и т.д. Всеми этими теоретическими положениями мы будем пользоваться при изучении социально-экономической статистики.

Дата добавления: 2014-01-03