Общие и частные решения рекуррентных соотношений

Общим решением рекуррентного соотношения (1) называется множество всех последовательностей, удовлетворяющих этому соотношению.

Частным решением соотношения (1) называется одна из последовательностей, удовлетворяющих этому соотношению.

Пример 1¢. Последовательность a_n = a ₀+ nd является общим решением соотношения a_n = a_{n -1}+ d. Это – формула общего члена арифметической прогрессии с разностью d и с начальным членом прогрессии a ₀.

Пример 2¢. Последовательность b_n = b ₀× qⁿ является общим решением соотношения b_n = b_{n -1} ×q. Это – формула общего члена геометрической прогрессии со знаменателем q ¹0 и с начальным членом прогрессии b ₀.

Пример 3¢. Так называемая формула Бине j _n =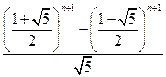является частным решением соотношения j _n =j _{n -2}+j _{n -1} при j₀=j₁=1.

3. Линейные рекуррентные соотношения. Соотношение вида

a_{n + k} + p ₁ a_{n + k -1}+…+ p_ka_n = h (n) (2)

где h (n) – функция от числа , а 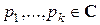, называется линейным рекуррентным соотношением.

Линейное рекуррентное соотношение называют однородным, если f (n)=0:

a_{n + k} + p ₁ a_{n + k -1}+…+ p_ka_n =0. (3)

Многочлен x^k + p ₁ x^{k -1}+…+ p_{k -1} x + p_k называется характеристическим для соотношения (2).

Корень a многочлена 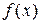называется простым, если 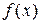делится на 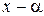, но не делится на .

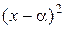Корень a многочлена 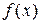называется кратным, если 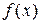делится на 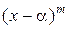, но не делится на , .

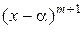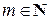При этом число 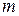называется кратностью корня .

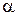Основная теорема алгебры: многочлен степени с комплексными коэффициентами имеет комплексных корней с учетом их кратности.

Теорема 1. Пусть характеристический многочлен однородного линейного рекуррентного соотношения (3) имеет n простых корней a₁, …, a _n. Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:

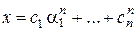, (4)

где c ₁,…, c_k Î C.

Доказательство. Легко проверить следующие два утверждения.

(a) Последовательность cxⁿ, где c Î C, является решением рекуррентного соотношения (3).

(b) Если последовательности a_n и b_n являются решениями соотношения (3), то последовательность a_n + b_n также является решением соотношения (3).

Из (a) и (b) следует, что любая последовательность вида (4) является решением соотношения (3).

Обратно, любое решение соотношения (3) имеет вид (4).

При n =0,1,…, k -1, из равенства (4) мы получим систему линейных уравнений относительно c ₁,…, c_k:

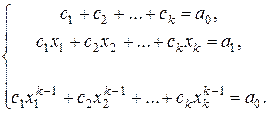(5)

Определитель системы (5) есть известный в алгебре определитель Вандермонда:

.

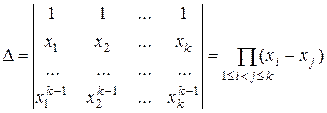Так как простые корни x ₁,…, x_k попарно различные, то D¹0. Значит, система (5) имеет (единственное) решение.

Задача 1. Найти общий член геометрической прогрессии по формуле (4).

Решение. Характеристический многочлен рекуррентного соотношения b_n = qb_{n -1} имеет вид 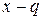. Поэтому .

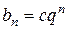Задача 2. Найти общее решение соотношения Фибоначчи a_{n +2}= a_n + a_{n +1}.

Решение. Характеристический многочлен рекуррентного соотношения a_{n +2}= a_n + a_{n +1} имеет вид 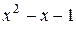. Поэтому .

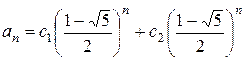Приведем без доказательства следующее обобщение теоремы 1.

Теорема 2. Пусть характеристический многочлен однородного линейного рекуррентного соотношения (3) имеет k корней: a₁ кратности 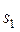, …, a _k кратности 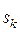, , 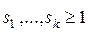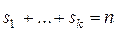. Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:

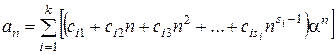, (6)

где .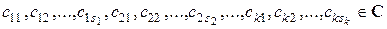

Задача 3. Найти общее решение соотношения .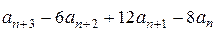

Решение. Характеристический многочлен 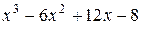имеет корень 2 кратности 3. Поэтому .

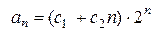Замечание. Общее решение неоднородного линейного соотношения (2) можно найти как сумму общего решения однородного линейного соотношения (3) и частного решения неоднородного линейного соотношения (2).

Дата добавления: 2014-01-03