Лекция № 9. Тема: разбиения на блоки и циклы

Тема: разбиения на блоки и циклы

Основные вопросы, рассматриваемые на лекции:

1. Разбиения множества на m блоков.

2. Число Стирлинга второго рода.

3. Разбиения перестановки на m циклов.

4. Число Стирлинга первого рода.

5. Факториальные многочлены.

Краткое содержание лекционного материала

1. Разбиения множества на m блоков. Говорят, что семейство множеств { M ₁,…, M_k } является разбиением множества M на k блоков M ₁,…, M_k, если M ₁,…, M_k – непустые, попарно не пересекающиеся, подмножества множества M и объединение множеств M ₁,…, M_k есть множества M. Число 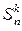(или S (n, k)) всех разбиений n -множества M на k блоков называется числом Стирлинга второго рода.

Пример 1. Перечислим все разбиения множества {1,2,3,4} на 2 блока:

{{1}, {2, 3,4}},

{{2}, {1, 3,4}},

{{3}, {1, 2,4}},

{{4}, {1, 2,3}},

{{1,2}, {3,4}},

{{1,3}, {2,4}},

{{1,4}, {2,3}}

Мы видим, что .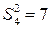

Примечание. Пусть | A |= m, | B |= n. Тогда число элементов:

· множества всех отображений множества A в B равно числу всех размещений с повторениями по m из n, то есть | B^A |= n^m;

· множества всех инъекций множества A в B равно числу всех размещений без повторений по m из n, то есть ;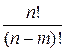

· множества всех биекций множества A на B равно числу всех размещений без повторений по m из n, то есть n!;

· множества всех сюръекций множества A на B равно произведению числа всех перестановок n -множества B на число всех разбиений n -множества B на m блоков, то есть n!.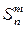

2. Число Стирлинга второго рода. Приведем рекуррентные формулы для числа Стирлинга второго рода:

;

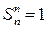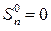, где n >0;

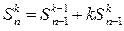, где n >0, 1£ k £ n.

Непосредственно число Стирлинга второго рода вычисляется по следующей формуле: .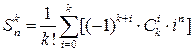

k n

Число всех разбиений n -множества M называется числом Белла B_n.

Ясно, что .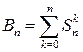

3. Разбиения перестановки на m циклов. Перестановка p m -множества M называется циклом, если p(x ₁)= x ₂, p(x ₂)= x ₃, …, p(x_{m -1})= x_m, p(x_m)= x ₁, где x ₁, x ₂, x ₃, …, x_{m -1}, x_m – все, различные, элементы множества M. Этот цикл обозначается через (x ₁ x ₂ x ₃… x_{m -1} x_m). Каждая перестановка состоит из конечного числа циклов, и эту перестановку можно записать в виде произведения циклов.

Пример 2. Перечислим все перестановки множества {1,2,3,4}, разбиваемые на 2 цикла:

(1)(234); (1)(243);

(2)(134); (2)(143);

(3)(124); (3)(142);

(4)(123); (4)(132);

(12)(34); (13)(24); (14)(23).

Числом Стирлинга первого рода (без знака) 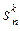(или s (n, k)) называется число разбиений n -множества B на k циклов.

4.Число Стирлинга первого рода. Приведем рекуррентные формулы для числа Стирлинга первого рода

;

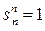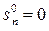, где n >0;

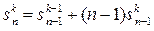, где n >0, 1£ k £ n.

k n

Ясно, что .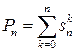

5. Факториальные многочлены. Любой многочлен от одной переменной можно представить как линейную сумму степеней переменной (базисных многочленов): , , , …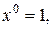

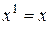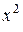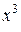Определим многочлены 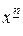, , 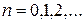которые также являются базисными: .

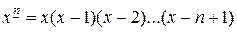Связь между двумя базисными многочленами устанавливается при помощи чисел Стерлинга первого и второго родов:

, .

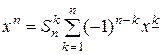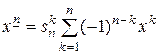Вместо «убывающих степеней» 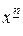можно рассматривать «возрастающие степени»: .

, .

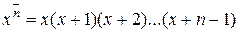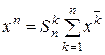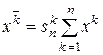Дата добавления: 2014-01-03