Лекция № 10. Тема: примеры рекуррентных соотношений

Тема: примеры рекуррентных соотношений

Основные вопросы, рассматриваемые на лекции:

1. Задача о ханойской башне

2. Разрезание пиццы

3. Задача Флавия

Краткое содержание лекционного материала

1. Задача о ханойской башне. Эту головоломку придумал французский математик Э. Люк в 1883 г. Формулировка задачи «Ханойская башня»:

Есть три стержня: A, B и C. На стержень A надето 8 колец: наверху самое маленькое, каждое следующее больше предыдущего, а внизу самое большое. Два других стержня пусты. Необходимо перенести все кольца со стержня A на стержень C, чтобы на стержне C кольца были в том же порядке, в котором они исходно находились на стержне A. Брать за один ход несколько колец нельзя. Кроме того, никогда нельзя класть большее кольцо поверх меньшего.

Рекуррентное отношение для решения задачи «Ханойская башня»: пусть 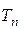– число ходов для решения задачи, где – число колец; тогда представим, что верхние 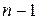колец перенесены на стержень 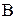(за 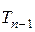ходов); тогда за один ход нижнее кольцо перенесем на стержень 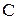; затем за 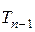ходов верхние 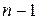колец на стержень 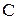; получим 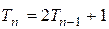. Значит, .

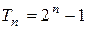Алгоритм: нечетный шаг – нужно перемещать верхнее кольцо, четный шаг – произведем единственно возможное перемещение оставшихся колец. Если перенумеровать кольца по порядку, то четные и нечетные кольца будут перемещаться в различных направлениях по кругу.

2. Разрезание пиццы. Впервые эта задача была решена в 1826 г. швейцарским математиком Я. Штейнером. Формулировка задачи: на какое максимальное число 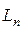областей можно разделить плоскость прямыми?

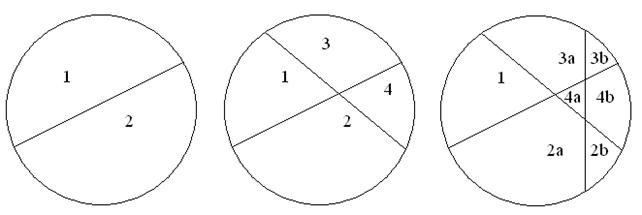
Рассмотрев случаи 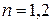можно подумать, что 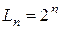. Однако уже при 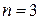получается 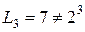. Рекуррентное соотношение: .

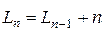Решение: .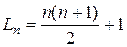

3. Задача Флавия основана на легенде, что отряд Флавия не пожелал сдаваться в плен блокировавшим пещеру превосходящими силам римлян. Воины, в составе сорока человек, стали по кругу и договорились, что каждые два воина будут убивать третьего, пока не погибнут все. При этом двое воинов, оставшихся последними в живых, должны были убить друг друга. Иосиф Флавий, командовавший этим отрядом, якобы быстро рассчитал, где нужно встать ему и его товарищу, чтобы остаться последними, но не для того, чтобы убить друг друга, а чтобы сдать крепость римлянам.

В более общей формулировке задачи участвует n воинов, стоящих по кругу, и убивают каждого m -го. Требуется определить номер k начальной позиции воина, который останется последним.

Дата добавления: 2014-01-03