Лекция № 11. Тема: графы и их способы задания

Тема: графы и их способы задания

Основные вопросы, рассматриваемые на лекции:

1. Виды графов

2. Степени вершин

3. Помеченные графы

4. Изоморфизмы графов

5. Матрицы смежности и инцидентности

Краткое содержание лекционного материала

1. Виды графов. Граф 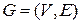состоит из двух множеств. 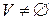. Элементы множества 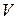называются вершинами, точками или узлами. 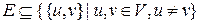. Неупорядоченные пары 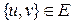называются ребрами, линиями или дугами.

Если 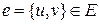, то говорят, что ребро 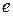соединяет вершины 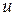и 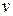. При этом вершины u и v называются концами ребра .

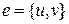Диаграмма графа G =(V, E) представляется в виде точек (или кружков) на плоскости, каждая из которых изображает вершину графа. Ребро графа 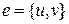изображается отрезком или дугой, соединяющей вершины u и v.

Диаграмму графа также называют графом.

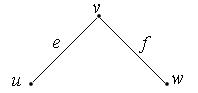
Две вершины графа u и v называются смежными, если они соединены некоторым ребром e графа. Вершина u и ребро e называются инцидентными, если u является концом ребра e. Два ребра e и f графа называются смежными, если они инцидентны одной и той вершине u графа.

(p, q)- граф – это граф с p вершинами и q ребрами

(p ³1 и ).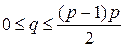

Тривиальный (p,0)-граф не содержит ни одного ребра.

Полный граф 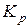– это 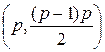-граф, содержащий все возможные ребра между 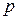вершинами.

Кроме графов (или неупорядоченных графов) рассматриваются и другие виды графов.

Мультиграф отличается от графа тем, что две вершины могут быть соединены двумя и более ребрами. При этом ребра, соединяющие две вершины в количестве двух и более, называются кратными.

Псевдограф отличается от графа тем, что в нем могут быть и кратные ребра, и петли (ребра, соединяющие вершины с самими собой).

2. Степени вершин. Степень 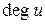вершины u – это число ребер, инцидентных вершине u. Вершина u называется изолированной (концевой), если ().

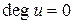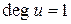Следующая теорема была первой в истории теории графов (1936 г.)

Теорема 1 (Л.Эйлер). Сумма степеней всех вершин (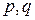)-графа равна удвоенному числу его ребер: .

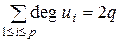Доказательство. При пересчете ребер, инцидентных всем вершинам, каждое ребро считается два раза.

Следствие. В графе число вершин с нечетными степенями четно.

Доказательство. Пусть вершины 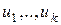имеют нечетные степени, а 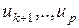вершины – четные степени. Тогда

.

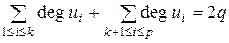3. Помеченные графы. Граф называется помеченным (или перенумерованным), если его точки обозначены попарно различными пометками.

Теорема 2. Существует 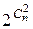помеченных графов с числом вершин n и 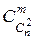помеченных (n, m)-графов.

Доказательство. Неупорядоченная пара { u, v } различных элементов u и v из множества V с числом элементов n есть сочетание без повторений из n элементов по 2. Поэтому число всех возможных ребер графа равно C_n ².

Каждый граф имеет множество ребер – некоторое подмножество множества из C_n ² элементов. Число всех подмножеств k -множества равно 2 ^k. Число всех 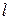-подмножеств k -множества равно .

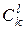4. Изоморфизмы графов. Графы G ₁=(V ₁, E ₁) и G ₂=(V ₂, E ₂) называются изоморфными, если существует биекция j: V ₁® V ₂, которая сохраняет отношение смежности между вершинами графа:

" u, v Î V ₁ ({ u, v }Î E ₁Û{j(u),j(v)}Î E ₂).

Пример изоморфных графов:

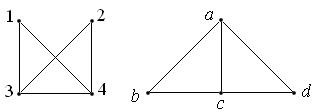
В этом примере биекция 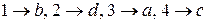является изоморфизмом графов.

Графы G ₁=(V ₁, E ₁) и G ₂=(V ₂, E ₂) могут быть неизоморфными, если:

1) ;

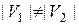2) ;

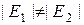3) для каждого 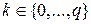графы имеют различные числа вершин степени .

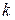Графы могут быть неизоморфными, даже если все перечисленные три условия выполнены:

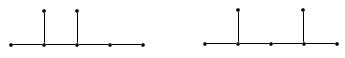
5. Матрицы смежности и инцидентности. Матрицей смежности графа 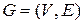называется матрица 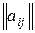, определяемая следующим образом: для всех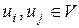

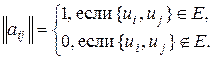
Матрицы смежности представляют собой квадратные матрицы с элементами 0 и 1, у которых по главной диагонали расположены нули. Матрица смежности графа симметрична относительно главной диагонали.

Матрицей инцидентности 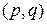-графа 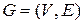называется прямоугольная 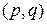-матрица 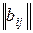, определяемая следующим образом: для всех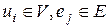

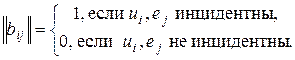
Дата добавления: 2014-01-03