Лекция № 13

Тема: эйлеровы и гамильтоновы графы

Основные вопросы, рассматриваемые на лекции:

1. Маршруты, цепи и циклы

2. Задача о кенигсбергских мостах. Эйлеровы графы

3. Задача о кругосветном путешествии. Гамильтоновы графы

4. Примеры (не)эйлеровых и (не)гамильтоновых графов

Краткое содержание лекционного материала

1. Маршруты, цепи и циклы. Маршрут (или путь) в графе – это чередующаяся последовательность вершин и ребер u ₁, p ₁, u ₂, p ₂, …, u_n, p_n, u_{n +1}, начинающаяся и кончающаяся вершиной, и каждое ребро p_i инцидентно вершинам u_i и u_{i +1}, где i =1,…, n.

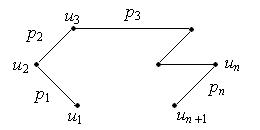
Этот маршрут обычно обозначается по вершинам: u ₁ u ₂… u_nu_{n +1}.

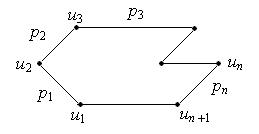
Маршрут называется замкнутым, если u_{n +1}= u ₁, и открытым, если u_{n +1}¹ u ₁.

Цепь – это открытый маршрут, в котором все ребра различны.

Простая цепь – это маршрут, в котором все вершины различны.

Если в маршруте два ребра равны, то равны и вершины – их концы. Значит, если все вершины маршрута различны, то и все ребра различны, поэтому простая цепь является цепью.

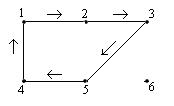
Пример 1. Рассмотрим граф с вершинами 1, 2, 3, 4, 5 и 6 с ребрами {1,2}, {1,4}, {2,3}, {2,4}, {2,5}, {3,5}, {3,6} и {5,6}.

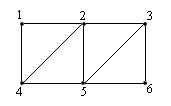
Приведем некоторые открытые маршруты в этом графе.

Маршрут 1253256 не является цепью.

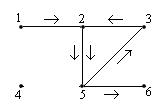
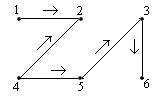
Маршрут 1245236 является цепью, но не является простой цепью.

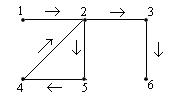
Маршрут 124536 является простой цепью.

Цикл – это замкнутая цепь. Простой цикл – это замкнутая простая цепь с числом вершин ³3.

Приведем некоторые замкнутые маршруты в графе примера 1.

Маршрут 12532541 не является циклом.

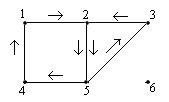
Маршрут 1235241 является циклом, но не является простым циклом.

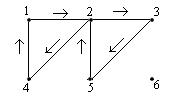
Маршрут 1235241 является простым циклом.

2. Задача о кенигсбергских мостах. Эйлеровы графы. В 1736г. Леонард Эйлер решил задачу о кёнигсбергских мостах.

Четыре части суши – два берега (точки A и D) и два острова (точки B и C) соединены семью мостами:

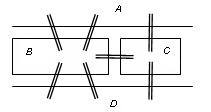
Надо прогуляться по замкнутому маршруту, так, чтобы пройти через каждый из мостов только один раз.

Решение задачи сводится к рассмотрению следующего мультиграфа и к поиску в нем замкнутого маршрута, проходящего через все ребра ровно по одному разу:

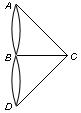
Эйлеров цикл в мультиграфе – это цикл, содержащий все ребра.

Граф называется эйлеровым, если содержит эйлеров цикл.

Пример эйлерова графа:

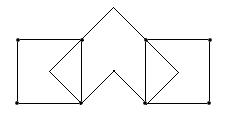
Граф называется связным, если любые его две вершины соединены некоторой цепью.

Теорема 1. Граф G эйлеров тогда и только тогда, когда граф G связный граф и степень каждой вершины графа G есть чётное число.

Доказательство. Если граф G эйлеров, т.е. содержит цикл, проходящий через все ребра графа G, то, значит, граф связный, а каждая вершина графа инцидентна четному числу ребер: вместе с каждым ребром – «входом» цикла в вершину должно быть ребро – «выход» цикла из вершины.

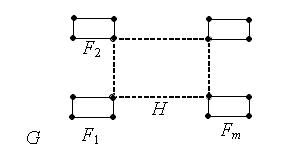
Обратно, индукцией по числу ребер доказываем, что если граф G связный, а каждая вершина графа инцидентна четному числу ребер, то в графе найдется подграф – эйлеров цикл. Поскольку граф связный и степени вершин – четные числа, то степень каждой вершины не меньше 2, значит, в графе G найдется хотя бы один цикл H. Разность G / H распадается на связные компоненты, содержащие тоже вершины с четными степенями, значит, по индуктивному предположению, содержащие эйлеровы циклы F ₁, …, F_m. Соединяя подходящим образом граф H с графами F ₁, …, F_m, получим эйлеров цикл в графе G.

3. Задача о кругосветном путешествии. Гамильтоновы графы. Задача Гамильтона: совершить кругосветное путешествие по ребрам додекаэдра, вершины которого символизировали крупные города Земли, при этом побывать в каждом городе ровно по одному разу.

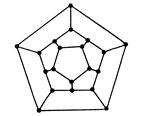
На рисунке – развертка додекаэдра.

Гамильтонов цикл – это простой цикл, проходящий через все вершины графа.

Гамильтонов граф – это граф, в котором содержащий хотя бы один гамильтонов цикл.

Полные графы – гамильтоновы.

Некоторые достаточные условия гамильтонова графа:

1) если степень каждой вершины 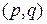-графа 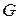не меньше 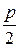, то граф 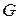является гамильтоновым (условие Дирака);

2) если сумма степеней любой пары несмежных вершин 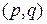-графа 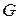не меньше 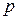, то граф 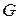является гамильтоновым (условие Оре);

3) если для любого числа 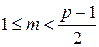число вершин 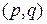-графа 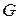, , 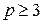со степенями не больших 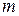, меньше чем 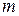, и для нечетного 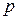число вершин степени 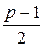не больше 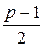, то то граф 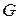является гамильтоновым (условие Поша).

Условие Поша обобщает условия Дирака и Оре.

Связный граф называется - связным, если для превращения его в несвязного графа нужно удалить не менее вершин.

Пример трехсвязного графа – колесо :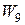

Связностью графа называется наименьшее число его вершин, удаление которых приводит к несвязному или тривиальному графу.

Легко видеть, что односвязные графы негамильтоновы.

Значит, гамильтоновы графы двусвязные, т.е. они связности 2 и более.

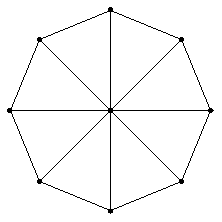
Тэта-графом называют граф, содержащий две вершины степени 3, соединенные тремя простыми попарно непересекающимися цепями длины не менее двух:

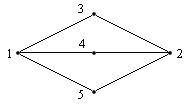
Если двусвязный граф содержит тета-граф, то он негамильтонов граф.

4. Примеры (не)эйлеровых и (не)гамильтоновых графов.

Приведем примеры графов, обладающих или не обладающих свойствами эйлеровости и гамильтоновости.

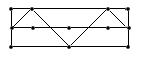
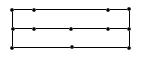
граф	гамильтонов	Не гамильтонов
эйлеров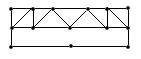
не эйлеров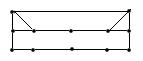

Дата добавления: 2014-01-03