Первый закон термодинамики

По исторически сложившейся традиции первый закон термодинамики часто трактуют как приложение всеобщего закона сохранения и превращения энергии к тепломеханическим процессам. Фактически же никакого различия между этими двумя законами нет, ибо первый закон термодинамики применяется не только при анализе тепломеханических процессов, но и в других случаях, например, в термохимии. Поэтому наиболее полно сформулировать его можно так: энергия изолированной термодинамической системы остается неизменной, независимо от того, какие процессы в ней протекают.

Для тепломеханических процессов это означает, что если в тепловом двигателе совершается прямой цикл, то сообщенное в этом цикле рабочему телу тепло 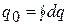должно быть в точности равно совершаемой им работе . Если бы оказалось, что 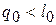, то можно было бы создать так называемый вечный двигатель первого рода, т.е. двигатель, совершающий работу без затраты внешней энергии. Равным образом, если бы оказалось, что 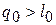, то имело бы место бесследное исчезновение энергии, равной 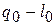. Оба предположения противоречат первому закону термодинамики, а из этого следует, что в данном случае .

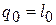С помощью аналогичного рассуждения можно показать, что в обратном цикле затраченная работа в точности равна полученному за ее счет теплу.

Рассмотрим теперь произвольный незамкнутый процесс 1–2. в общем случае для этого процесса 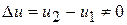, поэтому уравнение баланса энергии, выражающее неизменность общего запаса ее в термодинамически изолированной системе (состоящей в данном случае из источника теплоты, рабочего тела и объекта работы), принимает вид:

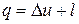. (1.11)

В правую часть этого равенства, называемого аналитическим выражением первого закона термодинамики, входят алгебраические величины: если внутренняя энергия увеличивается, то 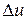>0, в противном случае 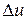<0. Равным образом, если работа совершается рабочим телом, то l >0, если она совершается над рабочим телом, то l <0. Поэтому и тепло q, находящееся в левой части равенства, является алгебраической величиной: если оно подводится к рабочему телу, то q >0, в противном случае q <0.

В развернутой форме аналитическое выражение первого закона термодинамики для процесса 1–2 принимает вид:

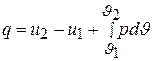, (1.12)

а в дифференциальной форме, соответствующей элементарному участку процесса,

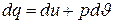. (1.13)

В этом выражении вместо внутренней энергии u может быть введена энтальпия i. Так, поскольку,

,

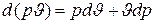то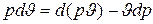

и тогда 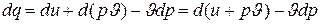(1.14)

или 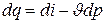, (1.15)

а в конечном виде .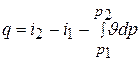

Интеграл – 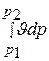, как энтальпия, представляет собой в общем случае чисто математическую величину и приобретает конкретное физическое содержание лишь при рассмотрении процессов, протекающих в потоке рабочего тела.

Дата добавления: 2014-01-03