Уравнение состояния идеальных газов

Тема № 2

Основные законы идеальных газов

Идеализация основных свойств тела, находящегося в газообразном состоянии – незначительности сил взаимного притяжения молекул и малости их объема, приводит к представлению об идеальном газе, у которого силы взаимного притяжения молекул вообще отсутствуют, а сами молекулы не имеют объема, т.е. представляют собой материальные точки.

Эти предпосылки позволяют получить теоретически выражение, называемое основным уравнением кинетической теории газов, или уравнение Клаузиуса:

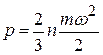, (2.1)

где р – давление газа;

n – число молекул;

m – масса молекул;

w – средняя скорость молекул.

Из этого уравнения с учетом зависимости (1.3) получаем:

.

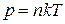Обозначив число молекул в одном килограмме газа через z, имеем:

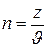
и тогда .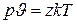

Написав это уравнение для двух произвольных состояний газа:

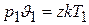и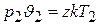

и разделив первое равенство на второе, а затем, объединив параметры, относящиеся к одному и тому же состоянию, находим:

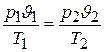. (2.2)

Поскольку состояния газа были приняты произвольно, очевидно, что величина

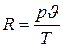
имеет одно и то же значение для любого состояния газа. Она называется газовой постоянной и имеет размерность

.

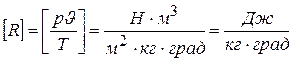Таким образом, термические параметры идеального газа в любом его состоянии связаны зависимостью

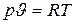, (2.3)

которая представляет собой термическое уравнение состояния идеального газа.

Впервые эта зависимость была получена Клапейроном и поэтому часто называется уравнением Клапейрона.

Умножая обе части равенства на массу газа М и учитывая, что 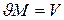, где V – полный объем этого газа, получаем уравнение состояния произвольного количества идеального газа:

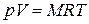. (2.4)

Дата добавления: 2014-01-03