Смеси идеальных газов

Если несколько газов, не взаимодействующих химически, поместить в общий сосуд, то благодаря хаотическому движению молекул, каждый из них равномерно распределится по всему объему сосуда и образуется газовая смесь.

Если обозначить концентрацию газа, т.е. количество молекул газа в единице объема через n, то согласно сказанному

,

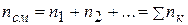т.е. концентрация газовой смеси равна сумме концентраций всех ее компонентов.

Поэтому для всей смеси в целом основное уравнение кинетической теории газов

,

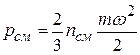где 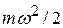– средняя кинетическая энергия молекул для всей смеси в целом, может быть представлено в виде формулы

.

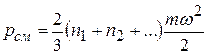Учитывая, что все компоненты находятся при одной и той же температуре, имеем:

,

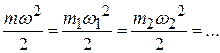откуда следует равенство

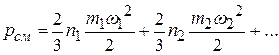
Каждое из слагаемых правой части представляет собой то давление, которое имел бы соответствующий компонент, если бы он один находился во всем объеме смеси при той же температуре, что и смесь. Такое давление называется парциальным давлением компонента.

Таким образом, давление газовой смеси равно сумме парциальных давлений ее компонентов, т.е.

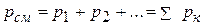. (2.14)

Это положение называется законом Дальтона.

Как указывалось, каждый компонент занимает весь объем смеси. Но если представить себе его заключенным в отдельный сосуд при давлении и температуре смеси, то занимаемый им объем будет меньше объема всей смеси. Это вытекает непосредственно из закона Бойля – Мариотта, согласно которому

,

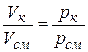где V_к – объем, который занял бы компонент, находясь отдельно от других компонентов при давлении и температуре смеси, называемый приведенным объемом данного компонента.

Последнее выражение можно записать в таком виде

.

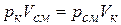Составляя такие выражения для каждого из компонентов, а затем складывая их левые и правые части, получаем

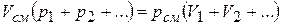
и, производя сокращение на основании закона Дальтона, находим окончательно

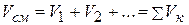(2.15)

т.е. объем газовой смеси равен сумме приведенных объемов ее компонентов.

Газовая смесь характеризуется своим мольным, объемным или массовым составом.

Мольный состав задается мольными долями компонентов, представляющими собой отношение количеств киломолей компонента Z_к в данной смеси к общему количеству киломолей смеси Z_см , т.е.

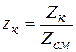, (2.16)

причем, поскольку .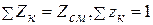

Объемный состав задается объемными долями компонентов, представляющими собой отношение приведенного объема компонента к объему всей смеси, т.е.

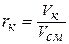, (2.17)

причем, поскольку .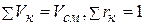

Наконец, массовый состав задается массовыми долями компонентов, представляющими собой отношение массы компонента к массе всей смеси, т.е.

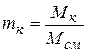, (2.18)

причем, поскольку .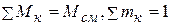

Хотя газовая смесь состоит из разнородных молекул, для применения к ней всех законов идеальных газов, а также для пересчета объемного состава в массовый и наоборот, в теорию газовых смесей введено понятие о средней (кажущейся) молекулярной массе смеси m_см , т.е. о молекулярной массе такого воображаемого однородного газа, который по своим физическим свойствам аналогичен рассматриваемой смеси.

Из самого определения киломоля вытекает равенство

,

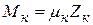справедливо для любого однородного газа. Поэтому по аналогии можно написать

.

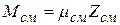Отсюда из равенства

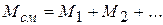
следует, что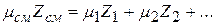

или ,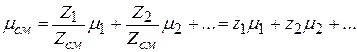

где z₁, z₂ … – мольные доли всех компонентов смеси.

Легко показать, что мольные доли компонентов численно равны объемным долям тех же компонентов. Действительно, обозначив объем одного киломоля любого газа при давлении и температуре смеси через 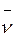, имеем

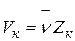и ,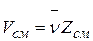

откуда .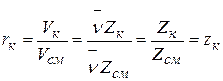

Таким образом, среднюю молекулярную массу смеси можно выразить через молекулярные массы компонентов и их объемные доли формулой

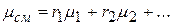(2.19)

Объемные доли удобно использовать также для вычисления парциальных давлений компонентов газовой смеси. Так, из уравнения

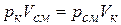
следует, что 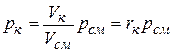. (2.20)

Пересчет объемного состава на массовый и наоборот производится на основе следующих соотношений между объемными и массовыми долями компонентов:

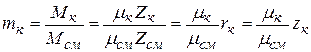; (2.21)

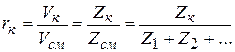, но ,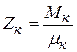

следовательно,

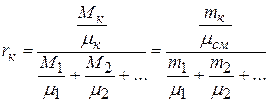. (2.22)

Чтобы к газовой смеси можно было применить уравнение состояния идеальных газов, следует знать ее газовую постоянную R_см. Если заданы массовые доли компонентов, то удобно применять формулу, вытекающую из следующих соображений.

Уравнение состояния для всей смеси в целом имеет вид

,

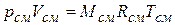а для каждого из компонентов может быть записано так:

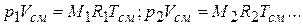
Учитывая, что ,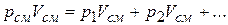

получаем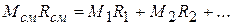

или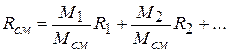

и окончательно

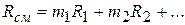(2.23)

Если заданы объемные доли компонентов, то удобнее всего использовать формулу (2.13), согласно которой

, Дж/(кг×град) (2.23)

где m_см – вычисляется по формуле (2.19).

Тема № 3.

Теплоемкость идеальных газов

Дата добавления: 2014-01-03