Нормирование погрешностей средств измерений

Средства измерений можно использовать только в том случае, если известны их метрологические свойства. Обычно их описывают путем указания номинальных значений тех или иных параметров и допустимых отклонений от них. Эти сведения приводят в технической документации на средства измерений.

Установление границ для отклонений реальных метрологических свойств средств измерений от их номинальных значений — нормирование метрологических свойств — предопределяет качество средств измерений. При изготовлении средств измерений, а затем в процессе эксплуатации проверяют, не выходят ли за установленные нормы реальные свойства средств измерений. И если какое-то из реальных свойств отклоняется от своего номинального значения больше, чем предусмотрено нормами, то средство измерения либо регулируют, либо переделывают, либо бракуют, либо запрещают к использованию.

Специфической метрологической характеристикой средств измерений является их погрешность. Сведения о погрешностях средств измерений необходимы для оценивания погрешности измерений. В связи с этим погрешности, возникающие в процессе измерений, приходится нормировать. При нормировании погрешностей средств измерений определяют пределы допустимых основной и всех дополнительных погрешностей, а также нормальные условия и допустимые отклонения от нормальных значений для всех влияющих величин. Одновременно устанавливают ряды пределов допускаемых измерений по точности и тем самым ограничивают их номенклатуру. Это упорядочение осуществляется путем установления классов точности средств измерений.

Класс точности — это обобщенная характеристика средств измерений, определяющая допустимые пределы для всех погрешностей этих средств измерений, а также и все другие свойства средств измерений, влияющие на их точность (см. табл.).

Форма выражения погрешности	Предел допускаемой погрешности	Обозначение классов точности
Приведённая погрешность, нормирующее значение выражено в единицах измеряемой величины		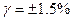1.5
Приведённая погрешность, нормирующее значение принято равным длине шкалы		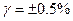0.5
Относительная погрешность постоянная		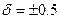0.5
Относительная погрешность возрастает с уменьшением измеряемой величины		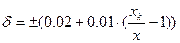0.02/0.01

Из всех перечисленных выше способов выражения погрешностей средств измерений лучшим является их выражение в виде относительных погрешностей, так как в этом случае указание допускаемого предела погрешности дает наилучшее представление о том уровне точности измерений, который может быть достигнут при применении данного средства измерений. Однако относительная погрешность обычно существенно изменяется вдоль шкалы прибора, поэтому ее применение для нормирования затруднительно.

Абсолютная погрешность часто удобнее относительной. В случае прибора со шкалой возможно нормирование предела допускаемой абсолютной погрешности с использованием одного числового значения для всей шкалы прибора. Но при этом трудно сравнивать приборы по точности, если они имеют разные диапазоны измерений, что отпадает при нормировании приведенных погрешностей.

Предел допускаемой абсолютной погрешности Δ может быть выражен одним значением (без учета знака) Δ = ± а в виде линейной зависимости

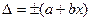(4)

(где х — номинальное значение меры, показание измерительного прибора или сигнал на входе измерительного преобразователя; a и b — постоянные величины)

или иным уравнением A = f(x); при более сложной зависимости (последняя обычно представляется таблицей или графиком).

Приведенная погрешность γ (в %) определяется формулой

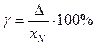(5)

где х_N — нормирующее значение.

Нормирующее значение считают равным:

- конечному значению шкалы прибора, если отметка находится на краю или вне шкалы;

- сумме конечных значений шкалы приборов (без учета знаков), если нулевая отметка находится внутри шкалы;

- номинальному значению измеряемой величины, если таковое установлено;

- длине шкалы, если шкала имеет резко сужающиеся деления. В этом случае погрешность и длину шкалы выражают в одних единицах.

Для приборов со шкалой, градуированной в единицах величины, для которой принята шкала с условным нулем (например, в °С), нормирующее значение принимают равным разности конечного и начального значений шкалы, т.е. диапазону измерений.

Предел допускаемой относительной погрешности δ (в %) должен выражаться одной из следующих формул:

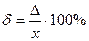(6)

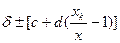(7)

где х_к — конечное значение диапазона измерений прибора или сигнала на входе преобразователя;

с и d — относительные величины.

Принятый вид формулы (7) придает первому слагаемому в правой части смысл относительной погрешности прибора при х = х_к. Второй член этого выражения характеризует возрастание относительной погрешности при уменьшении показаний прибора.

Таким образом, часть наименований разновидностей погрешностей закрепилась за погрешностями средств измерений, другая — за погрешностями результатов измерений, а некоторые применяются по отношению и к тем, и к другим.

Дата добавления: 2014-01-03