Теорема об изменении кинетического момента механической системы

Момент инерции твердого тела относительно некоторой оси равен сумме момента инерции тела относительно параллельной оси проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между этими осями.

Теорема о моментах инерции твердого тела относительно

параллельных осей (теорема Гюйгенса - Штейнера).

Доказательство. Выберем: в центре масс С тела начато ко­ординат осей xyz. Возьмем в теле точку 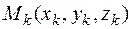массы 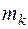. Проведем на расстоянии d от оси z ось 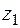. Тогда мо­мент инерции относительно этой оси

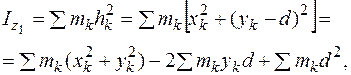
где 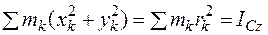- момент инерции тела, относительно оси, проходящей через центр масс;

;

,

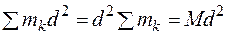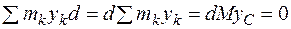т. к. 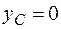(начало координат взято в центре масс). Тогда

.

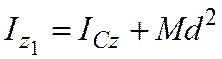Центробежные моменты инерции учитывают асимметрию в распределении масс, вычисляются относительно пары коор­динатных осей но формулам

.

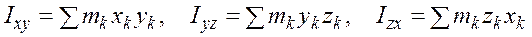В отличие от осевых центробежные моменты инерции могут быть положительными, отрицательными или равными нулю. Это зависит от выбора начала осей координат и их направления.

Ось, относительно которой центробежные моменты инер­ции, содержащие в своих индексах наименование этой оси, рав­ны нулю, называется главной осью инерции тела.

Главная ось инерции, проходящая через центр масс тела, называется глав­ной центральной осью инерции. Главными осями инерции твер­дого тела являются его оси симметрии.

.

Алгебраический момент количества движения матери­альной точки относительно некоторого центра О — скаляр­ная величина, взятая со знаком (+) или (-) и равная произ­ведению модуля количества движения 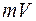на расстояние h (перпендикуляр) от этого центра до линии, вдоль которой направлен вектор :

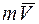Правило знаков: 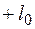— при движении точки против хода часовой стрелки; 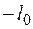- то же по ходу часовой стрелки

.

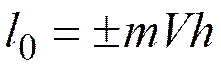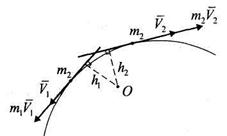
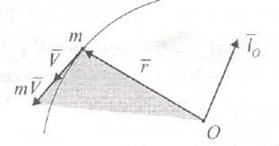
Векторный момент количества движения материальной точки относительно некоторого центра О — вектор, прило­женный в этом центре и направленный перпендикулярно плоскости векторов 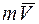и 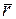в ту сторону, откуда движение точки видно против хода часовой стрелки.

Это определение удовлетворяет векторному равенству

.

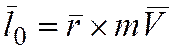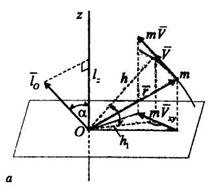
Моментом количества движения материальной точки от­носительно некоторой оси z называется скалярная величина 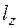, взятая со знаком (+) или (-) и равная произведению модуля 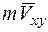проекции вектора 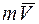количества движения на плос­кость, перпендикулярную этой оси, на перпендикуляр h, опу­щенный из точки пересечения оси с плоскостью на линию, вдоль которой направлена указанная проекция:

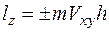lz.

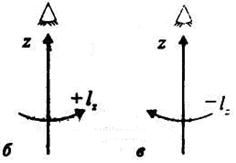
Правило знаков:

смотрим навстречу оси z

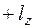— при движении точки против хода часовой стрелки

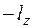- то же по ходу часовой стрелки.

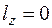, если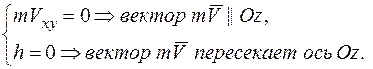

Кинетический момент механической системы относительно центра. Для k - й точки системы 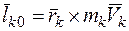— векторный момент. Для всей системы

.

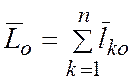Кинетическим моментом или глав­ным моментом количеств движения механической системы относитель­но некоторого центра называется геометрическая сумма моментов ко­личеств движения всех материаль­ных точек системы относительно то­го же центра.

Кинетический момент относительно оси. Для k-й точки 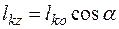— алгебраическая величина.

Для всей системы

.

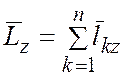Кинетическим моментом или главным моментом количеств движения механической системы относительно некоторой оси на­зывается алгебраическая сумма моментов количеств движения всех материальных точек систе­мы относительно той же оси.

Кинетический момент твердого тела, вращающегося во­круг неподвижной оси z с угловой скоростью .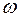

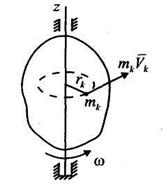
Для k – й точки тела

.

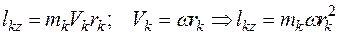Для всего тела

,

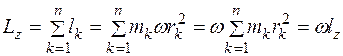где 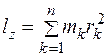— момент инерции тела относительно оси. Итак,

.

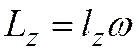Производная по времени от момента количества движе­ния материальной точки относительно некоторого непод­вижного центра равна моменту силы, действующей на точ­ку, относительно того же центра.

Доказательство. Пусть

.

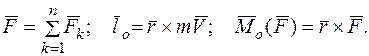
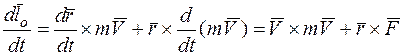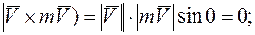
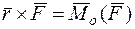— момент силы 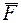относительно точки О. Итак,

.

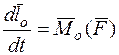Следствие. Если линия действия равнодействующей при­ложенных к точке сил все время проходит через неподвиж­ный центр, то момент количества движения материальной точки относительно этого центра остается постоянным.

Производная по времени от момента количества движе­ния материальной точки относительно некоторой оси равна моменту силы, действующей на точку, относительно той же оси.

Доказательство. Запишем в проекциях на оси декар­товых координат, учитывая, что

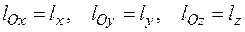и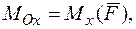

.

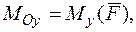
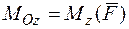Тогда

,

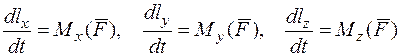где 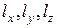— моменты количества движения материальной точки относительно осей координат; 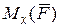, , 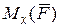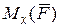— моменты силы относительно тех же осей.

Следствие. Если момент равнодействующей сил, дейст­вующих на материальную точку, относительно некоторой оси равен нулю, то момент количества движения матери­альной точки относительно той же оси остается величиной постоянной.

Дата добавления: 2014-01-03