На размер страхового запаса

Влияние характера распределения

Статистика сбыта в периоды между поставками

№ периода между поставками

Объём сбыта за период

Выполнив расчеты по приведенной выше формуле, полу­чим значение среднего квадратического отклонения

σ = 16,915.

Тогда размер страхового запаса составит

R =t∙a, R = 1,75 х 16,915 ≈ 30 единиц.

Таким образом, при стабильных, точно соответствующих планам поставках и колеблющемся, нормально распределенном сбыте наличие страхового запаса в 30 единиц обеспечит 96-про­центную готовность к поставке товаров со склада компании. В свою очередь, данная готовность обеспечит наилучшее соот­ношение между затратами на содержание запаса и возможны­ми потерями от дефицита.

Распределение нормальное

Условием применения приведенного порядка определении страхового запаса является нормальный характер распределе­ния значений случайной величины (в нашем случае значения потребности между двумя смежными поставками). Распределение является нормальным, если на величину признака дей­ствует множество взаимно независимых факторов, среди кото­рых нет ни одного с резко выделяющейся колеблемостью, т. е. роль каждого из факторов незначительна.

Методы проверки соответствия фактического распределе­ния случайной величины теоретическому закону распределения приведены в учебной литературе по математической статистике.

В первом приближении оценить принадлежность фактического распределения к нормальному можно, сопоставив значения трех параметров фактического распределения:

• мода — значение признака, наиболее часто встречающе­еся в исследуемой совокупности;

• медиана — значение признака, приходящееся на середи­ну ранжированной (упорядоченной) совокупности;

• среднее значение признака.

В случае близости перечисленных параметров распределе­ние является нормальным.

Распределение Пуассона

В случае если факторы, вызывающие отклонение значе­ния случайной величины от ее ожидаемого значения, действуют редко, но число таких факторов велико, случайная величина может быть распределена по закону Пуассона. В первом приближении оценить принадлежность фактического распределе ­ ния к пуассоновскому можно, сопоставив значения двух пара- метров фактического распределения:

• средняя величина вариации фактора;

• дисперсия вариаций фактора.

В случае близости перечисленных параметров может быть выдвинута гипотеза о том, что распределение является пуассоновским.

Равномерное распределение вероятности случайной вели­чины потребности в период между поставками.

Данный случай означает, что любое значение потребности, лежащее в пределах от известного минимального (q _мин) до известного максимального (q), имеет равную вероятность.

Формула для расчета величины страхового запаса в случае равномерного распределения имеет вид

R = (0,5- a)∙(q _макс - q _мин).

Как видим, изменение характера распределения оказывает существенное влияние на размер страхового запаса.

В заключение приведем высказывание автора ряда работ области исследования операций Н. Ш. Кремера: "Найти аналитически оптимальные значении точки запаса S₀ и объема пар­тии n удается только в относительно простых случаях. Если же система хранения запасов имеет сложную структуру (много видов хранимой продукции, иерархическая система складов), используемые стохастические модели сложны, а их параметры меняются во времени, то единственным средством анализа такой системы становится имитационное моделирование, позволяющее имитировать ("проигрывать") на вычислительной технике функционирование системы, исследуя ее поведение при различных условиях, значениях параметров, отражая их случайный характер, изменение во времени и т. п."^[55].

Глава 19. Системы контроля состояния запасов

19.1. Общая характеристика систем контроля состояния запасов

Управление запасами предусматривает организацию контроля их фактического состояния.

Контроль состояния запасов — это изучение и регулирование уровня запасов производственно-технического назначении изделий народного потребления и др. с целью выявления отклонений от норм запасов и принятия оперативных мер к ликвида­ции отклонений.

Необходимость контроля состояния запасов обусловле­на повышением издержек в случае выхода фактического раз­мера запаса за рамки, предусмотренные нормами запаса. Кон­троль состояния запаса проводится на основе данных учета за­пасов и может осуществляться непрерывно либо через опреде­ленные периоды.

На практике применяются различные методы контроля, которые можно классифицировать по следующим признакам:

• порядок проверки: периодическая или непрерывная;

• пороговый уровень запаса: наличие или отсутствие;

• величина заказываемой партии: одинаковая или разная.

Примерная классификация систем контроля состояния за­пасов представлена на рис. 67.

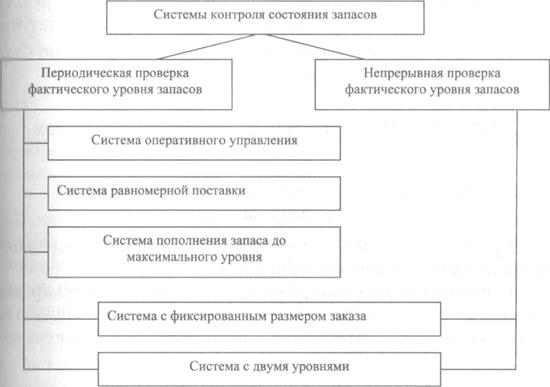Рис. 67. Классификация систем контроля состояния запасов

Контроль состояния запасов и формирование заказа поставщику может осуществляться по одной из представление ниже систем.

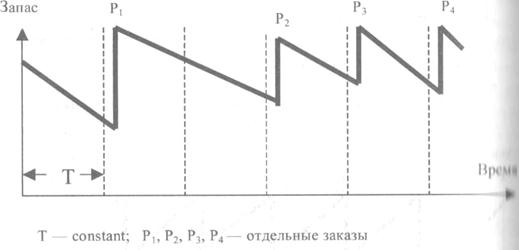Система оперативного управления. Через определения промежутки времени принимается оперативное решение: "заказывать" или "не заказывать", если заказывать, то какое количество единиц товара (рис. 68)^[56].

Рис. 68. Система оперативного управления

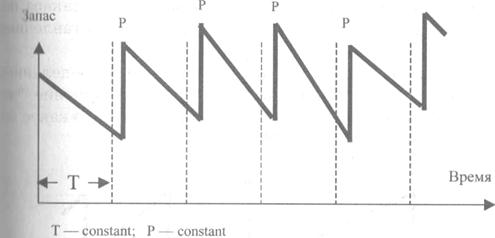Система равномерной поставки. Через равные промежутки времени заказывается постоянное количество единиц товара(рис. 69).

Рис. 69. Система поставки равного заказа через равные периоды времени

Система пополнения запаса до максимального уровня. При этом через равные промежутки времени заказывается партия, объем которой, т. е. число единиц товара, равен разности установленного максимального уровня запасов и фактического уровня запасов на момент проверки. Размер заказа увеличивается на величину запаса, который будет реализован за период выполнения заказа (рис. 70).

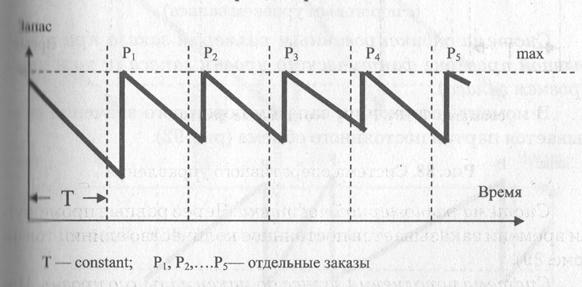
Рис.70. Система пополнения заказа до максимального уровня

Система с фиксированным размером заказа при периодической проверке фактического уровня запаса (с пороговым уровнем запаса). Фактический уровень запасов проверяется через рапные промежутки времени. Решение о заказе постоянного объёма товара принимается при условии, что товарный запас на момент проверки оказывается меньше или равен установлен­ому пороговому уровню товарных запасов. В противном случае принимается решение "не заказывать" (рис. 71)

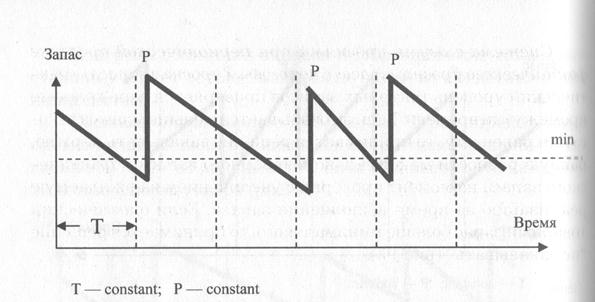
Рис.71. Система с фиксированным размером заказа при периодической проверке фактического уровня запаса (с пороговым уровнем запаса)

Система с фиксированным размером заказа при непрерывной проверке фактического уровня запаса (с пороговым уровнем запаса).

В момент достижения запасом порогового значения заказывается партия постоянного объёма (рис.72).

Система с двумя уровнями при периодической проверке фактического уровня запаса (с пороговым уровнем запаса). Фактический уровень товарных запасов проверяется через равные промежутки времени. Если он оказывается меньше минимально­го или равен ему, то принимается решение заказывать партию, равную разности максимального товарного запаса и фактиче­ского запаса на момент проверки с увеличением на ожидаемую реализацию за

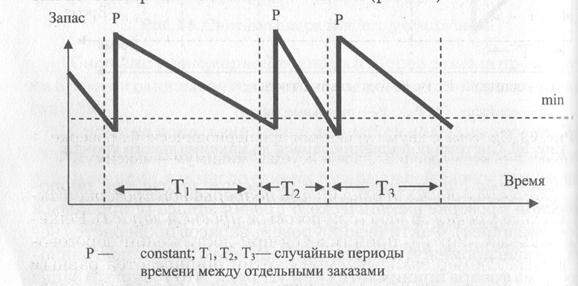
Рис.72 Система с фиксированным размером заказа при непрерывной проверке фактического уровня запаса (с пороговым уровнем запаса)

время выполнения заказа. Если фактический товарный запас больше минимального, то принимается решение "не заказывать" (рис. 73).

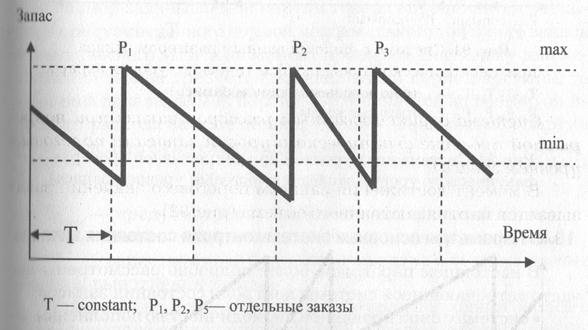
Рис.73. Система с двумя уровнями при периодической проверке фактического уровня запаса (система "минимум - максимум")

Система с двумя уровнями при непрерывной проверке фак­тического уровня запаса (с пороговым уровнем запаса). Решение заказать партию принимается при достижении порогового запаса. Размер заказываемой партии принимается равным разности максимального товарного запаса и порогового уров­ня с увеличением на ожидаемую реализацию за время выпол­нения заказа (рис. 74).

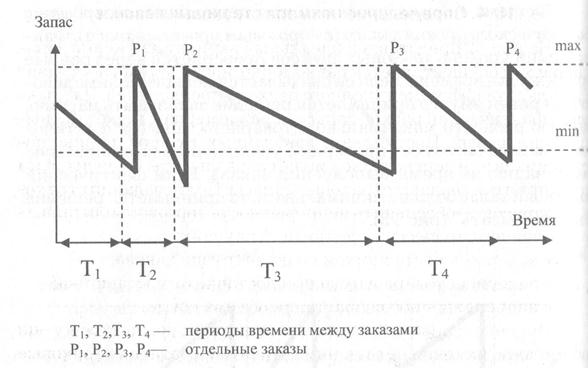
Рис. 94. Система двух уровней при непрерывной проверке

фактического уровня запаса (с пороговым уровнем запаса)

Дата добавления: 2014-01-03