N3 - число шариков с метками A и B.

Вероятность извлечения помеченного шарика равна:

p(AÈB) = (n1+n2+n3)/n

Произведем следующие допустимые преобразования:

p(AÈB) = (n1+n2+n3)/n + n3/n - n3/n = (n1+n3)/n + (n2+n3)/n - n3/n = p(A)+p(B)-p(AÇB)

Как нетрудно показать при помощи аналогичных преобразований, для случая трех разновидностей меток - A, B и C получается:

p(AÈBÈC) = p(A)+p(B)+p(C) -p(AÇB) -p(AÇC)-p(BÇC)+p(AÇBÇC).

Общая формула для произвольного количества типов меток:

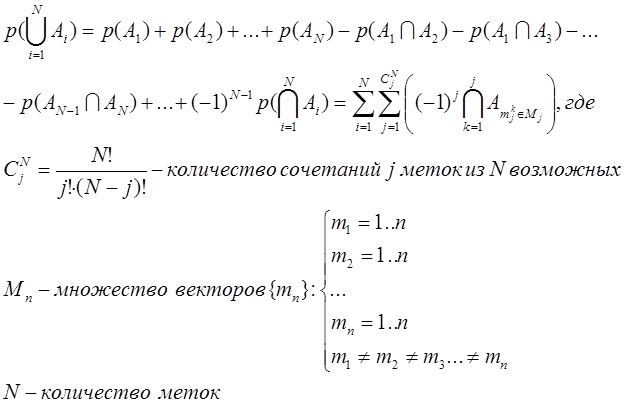
Следующее правило называется правилом композиции. Для описанного случая с метками двух типов справедливо:

p(A) = (n1+n3)/n = n3/n + n1/n = p(AÇB) + p(AÇ`B)

Или из определения условной вероятности

p(A) = p(A|B)*p(B) + p(A|`B)*p(`B)

3.2.5.2. Точные вероятностные рассуждения

Пусть имеется простейшая продукция

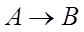
Необходимо выяснить истинность B.

Неопределенными могут быть 2 факта: истинность А и истинность самой импликации.

Пусть р(А)=0.9 и р(В|A) = 0.95

Из правила композиции:

p(B) = p(B|A)*p(A) + p(B|`A)*p(`A),

где p(`A) = 1 – р(А).

Подставив известные величины, получим:

p(B) = 0.95*0.9 + p(B|`A)*0.1 = 0.855 + p(B|`A)*0.1

Откуда можно заключить лишь, что p(B) лежит в пределах от 0.855 до 0.955

Конъюнктивная посылка

Рассмотрим импликацию, в которой две посылки объединены по И:

A ^ B -> C.

Типичной ситуацией является наличие сведений о вероятности A, B и импликации.

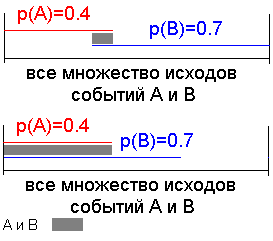
Например, p(A) = 0.8, p(B) = 0.7, p(C|AÇB) = 0.95.

Однако, записав при помощи правила композиции формулу для нахождения p(C), мы видим, что данных недостаточно:

p(C) = p(C|AÇB)* p(AÇ B) + p(C|~(AÇB))*p(~(AÇB))

Кроме того, в данной формуле отсутствуют p(A) и p(B). Существует методика оценки p(AÇB) при известных p(A) и p(B):

min {p(A), p(B)} ³ p(AÇB) ³ max{p(A) + p(B) – 1, 0}

Или в общем виде:

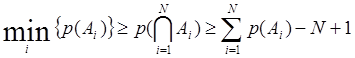
Дизъюнктивная посылка

Импликация, в которой посылки объединены по ИЛИ, менее жестка, чем предыдущая:

Если A ИЛИ B, то C.

Вероятность можно оценить следующим образом:

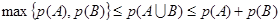
Т.е. попытки в условиях неопределенности оценить вероятность приводят к приближенности.

Основные два приема, которые можно рекомендовать для таких случаев:

Дата добавления: 2014-01-03