Автомат Мура

Определение автомата Мили.

Определение:Конечным автоматом называется набор из 5 объектов 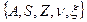, где:

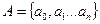- входной алфавит;

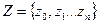­ выходной алфавит;

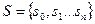­ множество внутренних состояний;

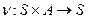­ функция перехода (в следующее состояние);

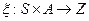­ функция выхода.

Таким образом, конечный автомат описывается тремя множествами и двумя функциями. Обе функции зависят от текущего внутреннего состояния и от входного символа, считываемого в данный момент времени. Автомат действует следующим образом. Конечный автомат, находящийся во внутреннем состоянии 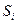, считывает входной символ 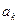. Функция 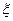принимает на паре 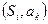значение 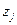- первый символ выхода. Функция 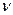принимает на паре 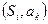значение 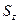, которое является следующим внутренним состоянием.

Пусть входящие символы записаны на входной ленте: **********. Автомат считывает с нее символы один за другим. По прочтению каждого символа автомат печатает выходной символ на выходной ленте и переходит в новое внутреннее состояние.

В определении подразумевается, что функци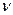и и 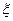в описании автомата М всюду определены, т.е. каждая пара из прямого произведения 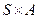задает их значения. Такое описание автомата является полным, т.е. если задано начальное состояние автомата, то он способен считывать любую последовательность входных символов и выдавать однозначно определенную цепочку символов на выходе.

Конечный автомат считается заданным, если заданы множества 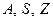(конечные), а также даны функции 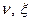или приведено их описание. Существует три способа задания конечных автоматов: таблица, диаграмма и матрица переходов.

Пример 1. Конечный автомат задан следующим образом:

, , , .

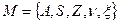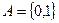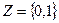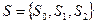Значения функций 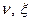заданы таблицей:

n:	(S0, 0)®S1,	x:	(S0, 0)®0,
	(S0, 1)®S0,		(S0, 1)®1,
	(S1, 0)®S2,		(S1, 0)®1,
	(S1, 1)®S1,		(S1, 1)®0,
	(S2, 0)®S0,		(S2, 0)®1,
	(S2, 1)®S2,		(S2, 1)®0.

Пусть на входе дана двоичная последовательность 0101 и автомат находится в состоянии 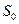, тогда на выходе получаем последовательность: 0010.

Этот автомат можно наглядно представить в виде диаграммы, которая, по сути, является ориентированным графом.

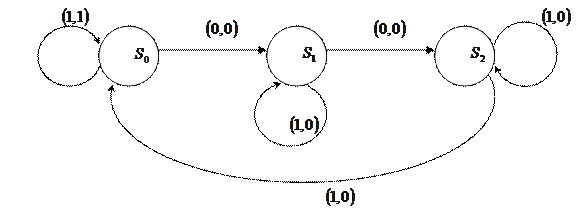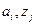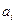Вершины этого графа помечены символами, обозначающими внутреннее состояние. Каждая дуга помечено парой символов (метка) , где - входной символ, вызывающий переход в следующее состояние, а 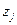- символ на выходе.

Второй способ описания автомата – таблица состояний. Этот способ часто приводится в виде условия задачи. Это просто табличное представление функци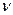й и :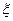

Текущее состояние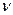

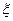
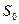
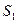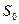
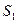
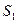
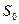
Таблица удобнее для вычислений, диаграмма - нагляднее. Например, по диаграмме легко обнаружить состояния, не достижимые из других состояний.

Кроме того, автомат можно задать с помощью матрицы. Такая матрица всегда будет квадратной по форме, а размерность её зависит от количества внутренних состояний. Каждая позиция матрицы отвечает за определённый переход из одного состояния в другое. Если какой-то переход существует, то на определённом месте матрицы должна стоять соответствующая метка. Если же некоторый переход отсутствует, то на этом месте в матрице стоит ноль.

Пример 2. По приведенному описанию построить конечный автомат. Задать его таблицей и диаграммой. Данный автомат проверяет четность числа считываемых единиц на входе из последовательности нулей и единиц, и выводит на печать символы чёт и нечёт в ответ на запрос, которому соответствует входной символ Q.

Согласно условию, алфавит на входе: 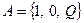, алфавит на выходе состоит из символов: 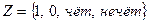. Множество внутренних состояний: 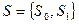, где содержание этих состояний следующее: 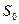- считано четное число единиц; 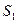- считано нечетное число единиц.

Анализируя работу автомата, можно составить таблицу:

Текущее состояние	n	x
		Q			Q
S0	S0	S1	S0			чёт
S1	S1	S0	S1			нечёт

Считав символ Q, автомат печатает "чет", если число ранее считанных единиц было четно, и "нечет" - если нечетно. Например, входная последовательность символов имела вид: 0110Q1110Q. Она будет переработана в последовательность: 0110четн1110нечет.

Диаграмма для данного автомата может быть составлена с помощью построенной таблицы:

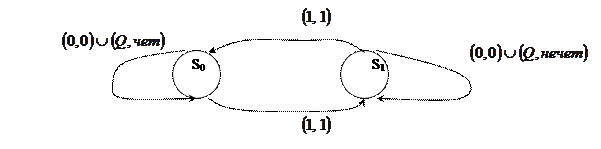
Любой конечный автомат Мили может быть преобразован в автомат, в котором выходной символ является функцией только состояния в настоящий момент.

Для этого полагают 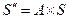- новый алфавит, 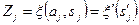, 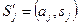. Отсюда получаем выражение для 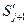: 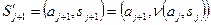или .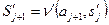

Такой автомат называется автоматом Мура. Так как автоматы Мили и Мура можно преобразовать друг в друга, то обычно достаточно рассматривать автомат Мили, тем более что число состояний у него меньше, чем у соответствующего автомата Мура.

Дата добавления: 2014-01-03