Теорема 1: Если , то либо , либо для подходящей строки имеем

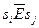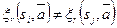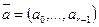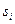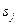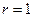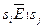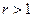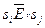Доказательство: Утверждение означает, что для подходящей строки . При необходимости мы можем укоротить входную строку так, чтобы входные строки, отвечающие и , отличались только последними символами. Пусть это уже сделано. Если после этого , то . Если же , то . Но 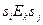при условии 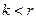. Таким образом, последние выходные символы автомата, считавшего 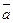, различны, если он исходил из начальных состояни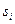й и 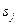соответственно. Чтобы выходы отличались, то есть 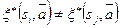должно быть выполнено условие: 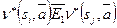. Иначе последний входной символ 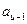даст один и тот же символ на выходе.

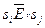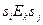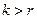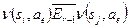Теорема 2: Если , но для всех , то для подходящего элемента .

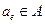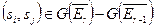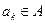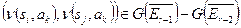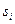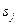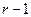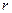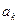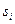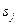Эту теорему можно переформулировать так: если , то для подходящего элемента имеем: . Эта теорема утверждает, что состояния и , эквивалентные относительно всех входных последовательностей длины , могут стать неэквивалентными относительно последовательностей длины только в том случае, когда имеется символ , переводящий и соответственно в состояния 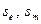, не эквивалентные относительно подходящей входной последовательности длины 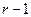. Это означает, что на 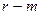шаге достаточно исследовать состояния в и установить, найдется ли пара 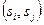, переходящая в пару 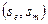со свойством 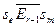. В этом случае .

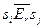Если мы уже определили 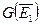, то 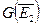состоит из 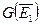и таких упорядоченных пар 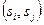, что для некоторого 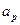имеем: 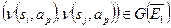. В общем случае нужно исследовать каждый раз только 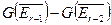. Таким способом мы сумеем рекуррентно определить 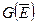и, наконец, 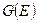- дополнение к 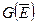в булевой алгебре подмножеств .

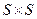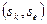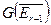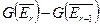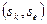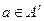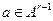Доказательство: Доказательство теоремы проводится непосредственно. Если пара лежит в , то она лежит в . Значит нужно рассмотреть лишь такие пары , что для некоторой строки имеем , а для всех строк имеем 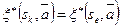. Но в точности те пары, которые переводятся в 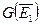, 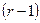-м входным символом 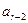и стало быть, в 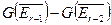, некоторым символом .

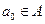Лемма: Если 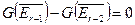, то 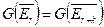для всех .

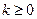Действительно, дальнейшие шаги не добавят новых пар состояний, т.к. согласно теореме 2, дополнение 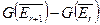состоит из тех пар, которые переводятся подходящим символом 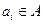в дополнение .

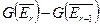Пример: Пусть задана таблица состояний некоторого автомата.

Текущее состояние	След. состояние 0 1	Выход 0 1
S1	S1 S2	1 0
S2	S1 S3	1 0
S3	S5 S1	1 0
S4	S4 S2	1 0
S5	S4 S3	1 1

Для этого автомата .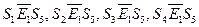

Иными словами: 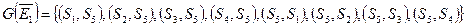. Первое разбиение на классы эквивалентности: 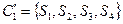, 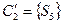. Вход 0 переводит 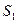в состояние 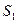, 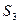в 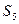: 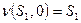, 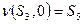. Поэтому вход 01 дает Следующие результаты:

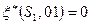и .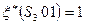

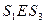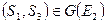Отсюда и . Аналогично: 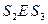и 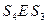, так что имеет место условие:

.

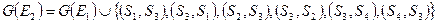Далее, входной символ 1 переводит состояние 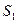в , а переводит в состояние 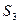. Другими словам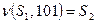и: и 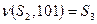. Поэтому 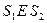, т.к. 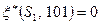и 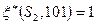. Аналогично: 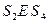, откуда следует:

.

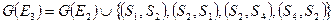Таким образом, 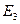разбивает 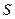на классы эквивалентности:

, , , .

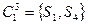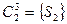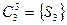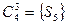Дальнейший перебор показывает, что 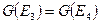. Таким образом, 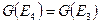и 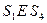, а остальные пары состояний неэквивалентны.

§4. Процедура минимизации конечных автоматов.

Актуальность проблемы минимизации конечных автоматов уже была приведена выше. В реальном устройстве (калькулятор, компьютер) увеличение числа внутренних состояний ведёт к увеличению числа микросхем, что в свою очередь может привести к росту стоимости, к более частым поломкам. Значит, уменьшение числа внутренних состояний автомата без ограничения его возможностей ведёт к экономии и надёжности в работе.

Процедура минимизации основана на рассмотрении отношений эквивалентности между упорядоченными парами. Рассмотрим автомат, заданный таблицей внутренних состояний:

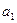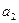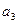
	Следующее сост.	Выход

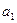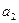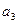
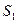
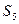
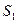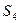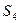
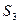
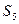
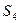
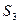
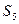
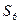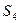
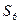
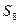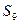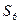
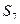
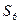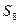
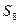
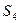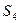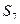
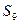
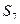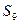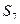
Процедуру минимизации начнем с нахождения множества пар эквивалентных состояни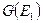й и 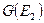. Введем в рассмотрение разбиение 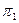, которое разобьет все состояния в таблице на два класса эквивалентности:

, .

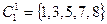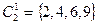В записи классов эквивалентности для краткости мы пишем 1 вместо S₁ и т.д. При составлении этого предварительного разбиения мы ориентируемся на выходную последовательность. Это разбиение определяет график 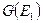соответствующего отношения эквивалентности. Т.к. отношение 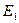рефлексивно и симметрично, то его график легко восстанавливается по множеству тех пар 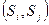, для которых 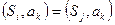при всех значений входного символа .

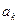Обозначим через 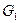подмножество, состоящее из пар 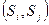, удовлетворяющих условию: 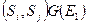, для которых 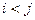. В общем случае через 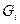будем обозначать множество упорядоченных пар 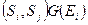со свойством 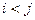. Для нашего разбиения имеем:

,

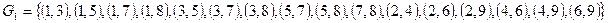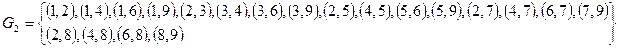
Т.к. 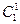и 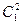- это классы эквивалентности относительно 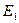, то имеем следующие соотношения: 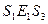, , 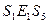, 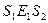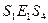и т.д.

Множество 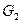состоит из элементов множества 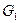и еще пар 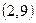, 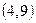и 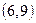. Например, входной символ 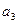переводит пару 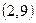в пару 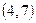, а эта последняя пара принадлежит 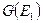. Добавление этих пар к 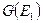определяет новое разбиение 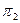на классы эквивалентности:

: , , .

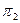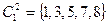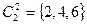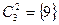Определим теперь множество 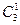. Оно состоит из элементов множества 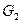и еще пар 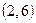и 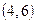. Например, входной символ 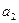переводит пару 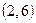в пару 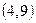, а эта последняя пара принадлежит множеству .

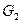При разбиении 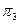имеем следующие классы эквивалентности:

, , , .

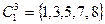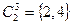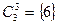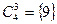Множество 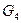состоит из элементов множества 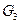и из пар 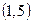, , 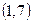, , 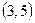, 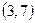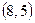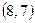. Поэтому разбиение 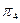состоит из следующих классов эквивалентности:

, , , , .

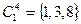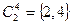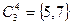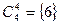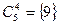Дальнейший перебор показывает, что 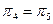и .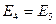

Конструкция покрывающего автомата теперь несложна. Каждый класс эквивалентности последнего разбиения становится состоянием нового автомата. Можно ввести новые обозначения. Например, 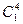обозначим через 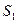, 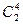- через и т.д. В итоге получается автомат с пятью состояниями, покрывающий наш первоначальный автомат с девятью состояниями. Поскольку выходы для каждого начального состояния в фиксированном классе эквивалентности не зависят от этого состояния при односимвольных входах, то таблица состояний нового автомата, в частности ее выходы, прямо считываются с таблицы состояний первоначального автомата.

Чтобы построить функцию перехода в следующее состояние, выберем то состояние 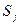в каждом классе 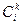, в котором некоторый элемент 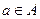входной последовательности переводит состояние 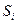в некоторое состояние из класса 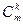. Положим 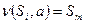. Заметим, что это предписание однозначно определено: все состояния 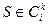переходят в состояние 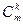после считывания символа из входной последовательности .

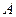На следующем примере показан результат этой процедуры, примененной к автомату, рассмотренному раньше.

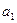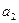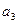
	Следующее сост.	Выход

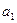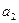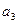
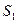
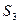
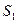
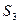
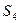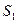
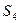
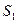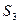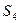
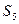
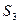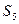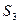
Этот автомат уже является минимальным. Это значит, что он не содержит эквивалентных состояний.

Замечание: На практике не обязательно перечислять все пары из множеств 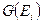и 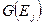. На каждом шаге процедуры достаточно смотреть, переводит ли некоторый входной символ 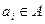пару 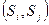из класса 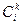в разные классы эквивалентност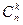и и 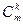. Если да, то на следующем шаге состояния 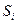и 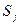следует развести по разным классам.

Пример. Рассмотрим конечный автомат с пятью состояниями, заданный таблицей.

	Следующее сост.	Выход

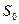
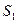
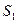
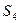
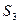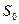
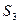
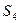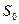
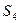
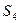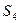
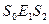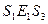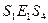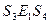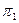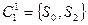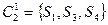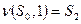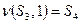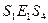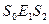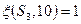Имеем , , , . Это приводит к разбиению : , . Тогда функция перехода при считывании единицы имеет вид , кроме того . Однако , поэтому (т.к. и ).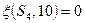

Следующее разбиение состоит из классов эквивалентности:

, , .

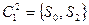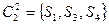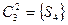Дальнейшего измельчения не происходит, т. к. функция 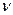переводит каждый элемент класса эквивалентности в тот же класс. Итак, состояния 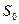и можно склеить в одно состояние `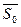, а состояния 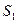и 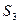- в состояние `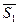. Состояние 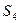обозначаем`теперь 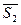. Новый минимальный автомат, покрывающий предыдущий, можно изобразить в виде:

	Следующее сост.	Выход

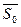
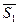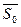
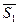
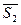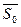
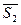
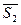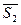
Дата добавления: 2014-01-03