Теоремы сложения и умножения вероятностей событий. Условная вероятность

• Определение. Суммой двух событий А и В называется событие С, состоящее в появлении или А, или В, или обоих событий: С = А + В.

• Теорема (о сложении вероятностей несовместных событий). Вероятность наступления одного из двух несовместных событий (безразлично какого) равна сумме вероятностей этих событий: Р (А + В) = Р(А) + Р(В),Т.е. вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Пример. Определить вероятность того, что при бросании игральной кости выпадет либо цифра 2, либо 5.

Решение. А={выпадет 2}, В={выпадет 5}. С = А + В = {выпадет либо 2, либо 5}, Причем события А и В – несовместные. Тогда Р(С) = Р(А + В) = Р(А) + Р(В) = 1/6+1/6= 1/3

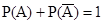
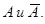Определение. Два несовместных события, образующих полную группу событий, называются противоположными событиями и обозначаются: Например, попадание и промах при одном выстреле.

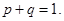
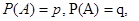Теорема. Сумма вероятностей противоположных событий равна 1:

Или, если то

• Определение. События А и В называются независимыми, если вероятность наступления одного события не зависит от того, наступило или нет другое событие.Например, 1) бросаются 2 монеты; 2) 2 баскетболиста бросают мяч в корзину.

• Определение. События А и В называются зависимыми, если вероятность наступления одного события зависит от того, наступило или нет другое событие.

• Определение. Произведением двух или нескольких событий называется событие, состоящее в совместном наступлении этих событий.

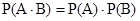Теорема (о вероятности произведения двух независимых событий). Вероятность произведения двух независимых событий (совместного наступления) равна произведению вероятностей этих событий:

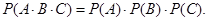• Для трех независимых событий:

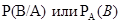• Определение. Если события А и В зависимы, то вероятность события В, вычисленная при условии, что наступило событие А, называется условной вероятностью В и обозначается Аналогично:

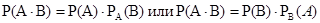Теорема умножения вероятностей зависимых событий. Вероятность совместного наступления двух зависимых событий (произведение двух зависимых событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие наступило:

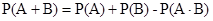Определение. Два события называются совместными, если наступление одного из них не исключает наступление другого в одном испытании.

Теорема сложения вероятностей совместных событий.

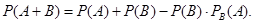
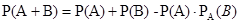
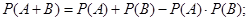Причем, если события А и В – независимы, то

Если А и В – зависимы, то или

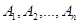Вероятность наступления хотя бы одного события

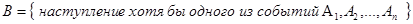
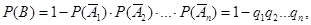Теорема. Вероятность наступления хотя бы одного из независимых событий равна разности между единицей и произведением вероятностей противоположных событий:

где событие

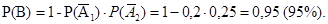Пример. Вероятность падания в корзину для одного баскетболиста равна 0,8, для другого – 0,75. Определить, вероятность попадания в корзину хотя бы одним баскетболистом.

Решение.

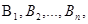Формула полной вероятности. Формулы Бейеса

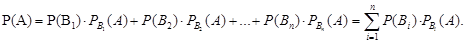Пусть требуется определить вероятность события А, которое может наступить при условии наступления одного из событий образующих полную группу несовместных событий, называемых гипотезами. Тогда вероятность события А определяется формулой полной вероятности:

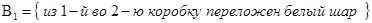
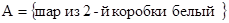Пример. В первой коробке 8 белых и 6 черных шара. Во второй коробке 7 белых и 5 черных шара. Из первой коробки во вторую переложили 1 шар, после чего из второй коробки наугад извлекли 1 шар. Найти вероятность того, что извлеченный из 2-й коробки шар белый.

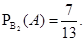
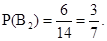
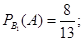
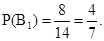Решение. Событие Гипотеза

Тогда вероятность того, что из 2-й коробки извлечен белый шар, равна Р(А)=4/7*8/13+3/7*7/13=53/91.

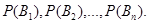
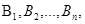Формула Бейеса (теорема о вероятности гипотез)

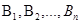Имеется полная группа несовместных гипотез вероятности которых до опыта известны:

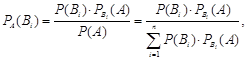Произведен опыт, в результате которого наступило событие А. Нужно определить, как изменятся вероятности гипотез

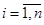в связи с наступлением события А.

Эти вероятности определяются с помощью формул Бейеса:

Дата добавления: 2014-01-03