Метод средних величин

4.

традиционные методы экономической статистики

Роль средних величин заключается в обобщении, т.е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности. D средний товарооборот на одного работающего является типической характеристикой торговой сети города.

Существует несколько видов средних:

Средняя арифметическая величина:

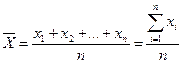
Так вычисляют среднюю величину, если известны все индивидуальные значения в совокупности. Если объем совокупности велик и представляет собой ряд распределения, используют значение средневзвешенной арифметической средней:

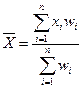
Сорт щебня					итого
Цена, д.е./м^3	xi	30,2	32,0	33,1	35,2
Объем реализации	wi

Средняя цена за м³ представляет собой распределения общей выручки от продажи всех сортов щебня по всем 1597 м³ реализации. Расчет показал, что средневзвешенная средняя арифметическая цена 1м³ щебня, реализованного за анализируемую неделю, составила 32,6 руб.

Средняя геометрическая позволяет сохранять неизменным не сумму, а произведение индивидуальных значений величины.

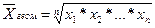
Основное применение средняя геометрическая находит при изучении темпов роста.

Средняя геометрическая дает наиболее правильный по содержанию результат и в тех случаях, когда требуется найти такое значение экономической величины, которое было бы качественно равноудалено как от ее максимального, так и от минимального значения.

Пример.

Год	I	II	III	IV
Темп роста цен	2.01	1.56	1.05	1.09

Темп роста цен за 4 года: 1,05*1,09*2,01*1,56=3,56

Средний темп роста по средней арифметической: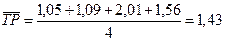

Однако, темп роста цен за год = 1,43*1,43*1,43*1,43=4,15 раза

Для того, чтобы данное противоречие не возникало, для расчета среднегодового темпа роста следует использовать формулу:

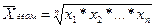
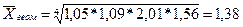
Пример применения средней геометрической при определении экономической величины, которая была бы качественно равноудалена как от ее максимального, так и от минимального значения.

Пример. В период наибольшей активности рентабельность деятельности дорожно-строительного предприятия - 36%, в период ежегодного спада (зимний сезон) – 2%. Какова средняя за год рентабельность работы этого предприятия? Определить по средней арифметической и по средней гармонической.

Средняя гармоническая используется в случаях, когда необходимо, чтобы при усреднении оставалась неизменной сумма величин, обратных индивидуальным значениям признака.

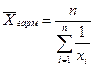
D дневная выработка рабочего – 520 деталей в смену. Ночная выработка – 450 деталей. При замене индивидуальных значений выработки на среднюю величину необходимо, чтобы неизменной величиной осталось время смены t. Поскольку обычно ночная смена короче дневной.

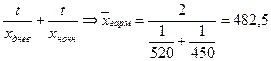
Средняя хронологическая используется для усреднения моментных показателей.

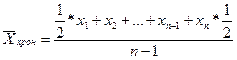
Графоаналитический метод определения средней позволяет получить результаты, соответствующие среднему значению труднофиксируемых и неустойчивых факторов.

	№ наблюдений
Количество отверстий на м^2, шт
Расход времени на объем работ, мин.	3,2	3,9	4,2	4,8	6,8	7,1

1) на графике по оси Х – шкала числовых значений фактора (число отверстий);

по оси У – шкала расхода времени.

2) значения расхода времени наносим на график в виде точек и по их расположению принимаем в качестве обобщающей соответствующую теоретическую линию

3) у=а+bx

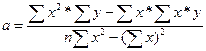
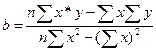
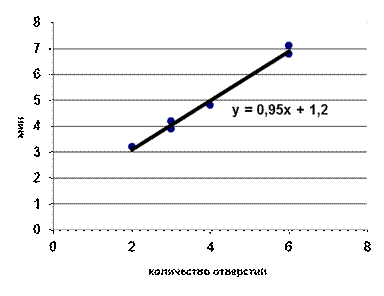
4) по полученному уравнению прямой можно установить средние значения расходов времени для любого объема работ.

Дата добавления: 2014-01-03