Степень комплексного числа

3.1. Натуральная степень комплексного числа

n-й натуральной степенью комплексного числа z называется комплексное число, полученное в результате умножения числа z на себя n раз:

.

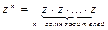n-ю степень числа z обозначают zⁿ.

Число z называется основанием степени, а натуральное число n – показателем степени.

n-я степень комплексного числа, записанного в тригонометрической форме

z = r×(cos j + i×sin j),

вычисляется по формуле Муавра:

zⁿ = rⁿ×(cos n×j + i×sin n×j).

Замечание. Наряду с алгебраической и тригонометрической формами представления к.ч. часто используется так называемая показательная (экспоненциальная) форма. Она основана на формуле Эйлера

.

Показательной (экспоненциальной) формой представления к.ч. называется выражение

,

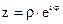где r – модуль к.ч., а j = arg z – главное значение аргумента к.ч.

3.2. Корень n-й степени из комплексного числа

Под корнем n-й степени из к. ч. z понимается множество к. ч., являющихся решениями уравнения

wⁿ = z (2)

Корень n-й степени из комплексного числа z обозначается символом .

Все корни n-й степени из комплексного числа z, заданного в тригонометрической форме

z = r×(cos j + i×sin j),

вычисляются по формуле

,

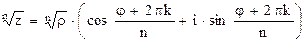где k = 0, 1, …, n–1.

Геометрически все корни n-й степени из к. ч. z = r×(cos j + i×sin j) изображаются точками, лежащими на окружности с центром в начале координат, радиус которой равен nÖr, а центральные углы между радиусами, проведенными в соседние точки, равны 2p/n.

Пример. Вычислить корни четвертой степени из числа –1.

Решение. Число (–1) в тригонометрической форме может быть записано так: – 1 = 1 × (cos p + i×sin p).

Корни четвертой степени из числа (–1) – это комплексные числа

,

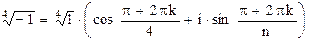где k=0, 1, 2, 3, т.е. комплексные числа

, ,

, .

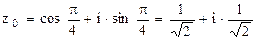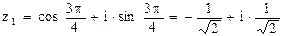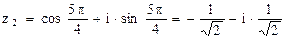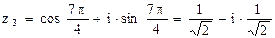Аналогичным образом в множестве комплексных чисел можно вычислить корень n-й степени из любого действительного числа. При этом хотя бы один корень из положительного действительного числа будет действительным.

Вариант в каждой группе соответствует алфавитному списку группы по порядку нумерации!!! К ЭКЗАМЕНУ!!!

Сдать 2 октября в тетрадке отдельной!!!

Индивидуальное домашнее задание по теме «Комплексные числа»

1. Вычислить число .
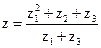2. Построить на комплексной плоскости числа .
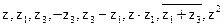3. Представить в показательной, экспоненциальной и тригонометрической форме заданные комплексные числа, изобразить их на комплексной плоскости.
4. Решить уравнение, корни изобразить на комплексной плоскости.

Вариант	Задачи №1,2
Z1	Z2	Z3
	4+3×i	–18–15×i	–4–6×i
	5–4×i	–30+24×i	–4–5×i
	–3–3×i	–8–24×i	2+4×i
	3–4×i	–6+20×i	–5+2×i
	–6×i	–6–30×i	–6–3×i
	2–3×i	38–3×i	–6×i
	1+4×i	–4+6×i	2–3×i
	–3–2×i	–6–18×i	2+3×i
	3–i	–2–16×i	–6–3×i
	–2–3×i	11–i	6–3×i
	–2–4×i	16–20×i	2–2×i
	2+2×i	8–2×i	3–3×i
	–1+i	2+32×i	4+3×i
	1–2×i	12+6×i	–3+i
	–6+2×i	–18–4×i	6+3×i
	–2+i	15–25×i	3+4×i
	–1–2×i	–8–16×i	–3+4×i
	–2+5×i	–6+30×i	–3–5×i
	4+3×i	12–24×i	–1–6×i
	–5–3×i	–9–3×i	–1+3×i
	–3–3×i	1–3×i	–1+5×i
	3–i	1–i	–3–i
	–1–2×i	18–4×i	–5–2×i
	–5–i	2+6×i	1–2×i
	5–6×i	–3+11×i	4+4×i
	–2+4×i	–8+14×i	5+2×i
	1–5×i	24+18×i	–2+i
	3+2×i	16+4×i	–5–5×i
	1+i	–2–16×i	–3+2×i
	–2+2×i	4+12×i	2–3×i

Вариант	Задача №3	Задача №4
Z1	Z2
	–5 + 5iÖ3	1 + 3i	8z^2 + 8z + 7 = 0
	2i	–6 –3i	3z^2 + 3z + 2 = 0
	3 – 3iÖ3	–3 – 4i	6z^2 – 2z + 4 = 0
	6 – 6iÖ3	3 – i	7z^2 – 4z + 3 = 0
	1 – i	–1 + 2i	z^2 – 4z + 6 = 0
	3 + 3i	6i – 1	4z^2 + 4z + 3 = 0
	–1 – iÖ3	–2 + i	3z^2 – 2z +1 = 0
	1 – iÖ3	1 – 5i	4z^2 – 8z + 7 = 0
	–5Ö3 – 5i	6 – i	z^2 + z + 3 = 0
	Ö3 – i	1 + 2i	z^2 + z + 7 = 0
	–5i	3 + 6i	5z^2 + z + 1 = 0
	4Ö3 + 4i	–4 – 5i	4z^2 + 6z + 4 = 0
	–2 –2iÖ3	–5 –2i	5z^2 + 5z + 2 = 0
	1 + i	3 + i	-3z^2 +7z + 5 = 0
	–2	–6 + 5i	2z^2 + 6z + 5 = 0
	1 + iÖ3	4 – 2i	z^2 – 3z + 8 = 0
	6Ö3 + 6i	5 – 4i	3z^2 + 4z + 4 = 0
	–2 –2i	–5 +2i	5z^2 + 6z + 2 = 0
	Ö3 - i	3 – 5i	3z^2 + 2z + 5 = 0
	4 – 4i	4 + 6i	5z^2 + 4z + 3 = 0
	–2 + 2iÖ3	2 – 6i	4z^2 – 5z + 4 = 0
	–3Ö3 + 3i	–3 + 4i	z^2 – z + 2 = 0
	2 – 2iÖ3	–6 + i	3z^2 –2z + 2 = 0
	Ö3/3 – i	–3 + 2i	7z^2 –4z + 7 = 0
	1 + iÖ3	2 – 4i	z^2 + 4z + 8 = 0
	-Ö3/3 - i	5 – i	8z^2 – 6z + 5 = 0
	2Ö3 – 2i	–5 –3i	z^2 – 2z + 4 = 0
	(–1 – iÖ3)/4	–1 –4i	z^2 + z + 4 = 0
	–1/2 + iÖ3/2	3 – 2i	2z^2 + z + 3 = 0
	–3i	2i – 1	7z^2 + 3z + 3 = 0

Дата добавления: 2014-01-03