Взаимная корреляционная функция

Взаимные корреляционные функции сигналов

Взаимная корреляционная функция (ВКФ) разных сигналов (cross-correlation function, CCF) описывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной). Обобщая формулу (6.1) автокорреляционной функции на два различных сигнала s(t) и u(t), получаем следующее скалярное произведение сигналов:

B_su(t) =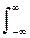s(t) u(t+t) dt. (6.14)

Взаимная корреляция сигналов характеризует определенную корреляцию явлений и физических процессов, отображаемых данными сигналами, и может служить мерой “устойчивости” данной взаимосвязи при раздельной обработке сигналов в различных устройствах. Для конечных по энергии сигналов ВКФ также конечна, при этом:

|B_su(t)| £ ||s(t)||×||u(t)||,

что следует из неравенства Коши-Буняковского и независимости норм сигналов от сдвига по координатам.

При замене переменной t = t-t в формуле (6.2.1), получаем:

B_su(t) =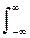s(t-t) u(t) dt =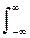u(t) s(t-t) dt = B_us(-t).

Отсюда следует, что для ВКФ не выполняется условие четности, B_su(t) ¹ B_su(-t), и значения ВКФ не обязаны иметь максимум при t = 0.

Это можно наглядно видеть на рис. 6.6, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (6.14) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)). При t=0 сигналы ортогональны и значение B₁₂(t)=0. Максимум В₁₂(t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t).

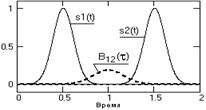
Рис. 6.6. Сигналы и ВКФ

Одни и те же значения ВКФ по формулам (6.14) и (6.14') наблюдаются при одном и том же взаимном положении сигналов: при сдвиге на интервал t сигнала u(t) относительно s(t) вправо по оси ординат и сигнала s(t) относительно сигнала u(t) влево, т.е. B_su(t) = B_us(-t).

На рис. 6.7 приведены примеры ВКФ для прямоугольного сигнала s(t) и двух одинаковых треугольных сигналов u(t) и v(t). Все сигналы имеют одинаковую длительность Т, при этом сигнал v(t) сдвинут вперед на интервал Т/2.

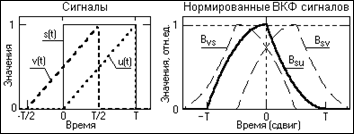
Рис. 6.7. Взаимноковариационные функции сигналов

Сигналы s(t) и u(t) одинаковы по временному расположению и площадь "перекрытия" сигналов максимальна при t=0, что и фиксируется функцией B_su. Вместе с тем функция B_su резко асимметрична, так как при асимметричной форме сигнала u(t) для симметричной формы s(t) (относительно центра сигналов) площадь "перекрытия" сигналов изменяется по разному в зависимости от направления сдвига (знака t при увеличения значения t от нуля). При смещении исходного положения сигнала u(t) влево по оси ординат (на опережение сигнала s(t) - сигнал v(t)) форма ВКФ остается без изменения и сдвигается вправо на такое же значение величины сдвига – функция B_sv на рис. 6.7. Если поменять местами выражения функций в (6.14), то новая функция B_vs будет зеркально повернутой относительно t=0 функцией B_sv.

С учетом этих особенностей полное ВКФ вычисляется, как правило, отдельно для положительных и отрицательных запаздываний:

B_su(t) =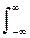s(t) u(t+t) dt. B_us(t) =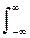u(t) s(t+t) dt. (6.14')

Дата добавления: 2014-01-03