Нормальное распределение

Наиболее распространенным на практике является нормальный закон распределения. Нормальным распределением (или коном Гаусса) называется распределение непрерывной случайной величины, плотность которой определяется по формуле

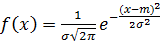(21)

где: m- и σ² параметры распределения. (σ² -- дисперсия случайной величины m = M(x)-- ее математическое ожидание)

е = 2,72,

π= 3,14.

Непрерывная случайная величина Х, может принимать как положительные, так и о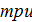цательные значения во всем диапазоне возможных значений от,.

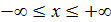Кривая плотности распределения нормального распределения (кривая Гаусса) имеет симметричный колоколообразный вид с максимальной ординатой при х = М(х) =m, равной 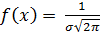. По мере удаления в обе стороны от точки x=m плотность распределения падает и при 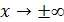кривая асимптотически приближается к оси абсцисс.

Функция нормального распределения

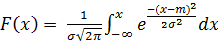(21)

Для краткой записи нормального распределения с параметрами т и σ используют обозначение N(m, σ) Можно доказать, что параметр т равен математическому ожиданию, а параметр σ — стандартному отклонению случайной величины X.

Влияние параметров m=M(x) и σ² на плотность и функцию нормального распределения можно проследить на рисунке.2/

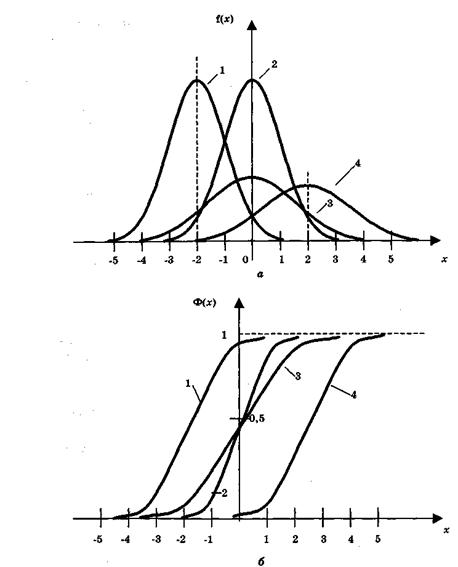
. Рисунок. 2 Кривые плотности (а) и функции (б) нормального распределения для следующих значений параметров:

1 – m=2; σ² = 0.25

2 - m=0; σ² = 1,0

3 - m=0; σ² = 0,25

4 - m=2; σ² = 1

С ростом величины математического ожидания m обе функции сдвигаются параллельно вправо, не изменяя своей формы.

С уменьшением дисперсии σ² кривая плотности распределения вытягивается вверх и одновременно сжимается с боков, а кривая функции распределения становится более крутой.

Так как плотность нормального распределения одномодальна и симметрична относительно математического ожидания m, то M(x) = m одновременно является медианой и единственной модой, т.е.

m = M(x) = M_o = M_e

Дата добавления: 2014-01-03