Стандартное нормальное распределение

Рассмотрим частный случай, когда параметры распределения m = 0.σ = 1. Нормальное распределение N(0;1) называется стандартным нормальным распределением. В этом случае плотность распределения

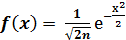(22)

Кривая распределения, построенная по формуле стандартного нормального распределения имеет колоколообразныи вид, вертикальная ось является осью симметрии, горизонтальная — асимптотой. Максимальное значение ординаты равно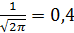

При значениях аргумента х = ± 3 значения функции близки к нулю: при общей площади под кривой распределения, равной единице, в этом диапазоне лежит 99,73%. Заметим, что в диапазоне х = ± 2 лежит 95,44% площади под кривой распределения, а в диапазоне х = ±1 — 68,26%.

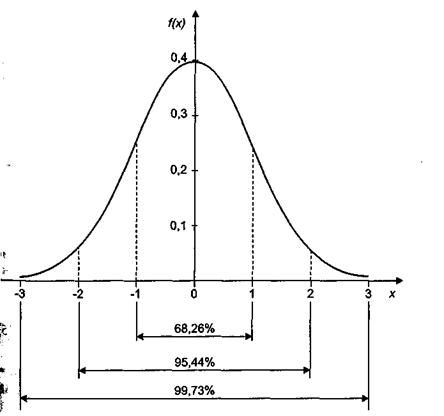
Рисунок 3.- Кривая стандартного нормального распределения

При изменении параметра т график сдвигается вправо или влево так, что прямая х= т — ось симметрии

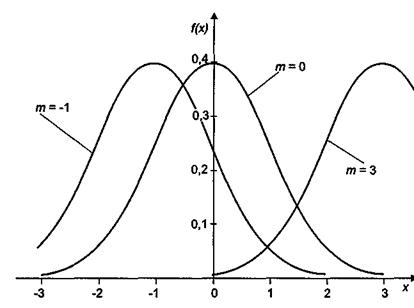
Рисунок 4- Влияние параметра т на вид кривой нормального распределения

При увеличении параметра σ максимум кривой распределения снижается, при уменьшении, а кривая вытягивается вверх, при этом по условию нормировки площадь под кривой распределения остается постоянной (и равной единице)

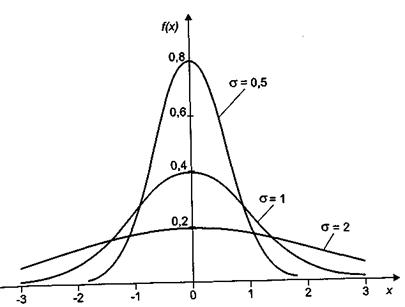
Рисунок 5 – Влияние параметра σ на вид кривой нормального распределения.

Вновь рассмотрим стандартное нормальное распределение N(0,1). Функция такого распределения иногда называется функцией Лапласа, она имеет специальное обозначение Ф(х).Можно записать уравнение

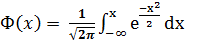(23)

Эnа функция табулирована. Например, Ф(2,48) = = 0,9934. График функции показан на рис.

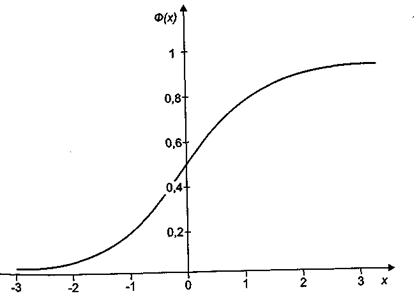
Рисунок 6 - График функции стандартного нормального распределения

Из симметрии графика вытекает соотношение

Ф(-х) = 1-Ф(х)

Табулированы и квантили нормального распределения

Квантиль нормального распределения порядка р — это число u_p, для которого Ф(u_p) = p. Например,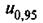=1,645

Из симметрии графика функции стандартного нормального распределения и формулы вытекает полезное соотношение для квантилей:

u_1-p = u_p

Можно установить связь между функцией распределения F(x) для распределения N(m,σ) и функцией стандартного нормального распределения:

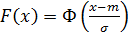(24)

Вероятность попадания нормально распределенной случайной величины в интервал от x₁ до x₂ определяется по формуле

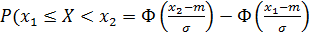(25)

Часто в расчетах надо найти вероятность того, что случайная величина Х не слишком сильно отклонится от своего математического ожидания m:

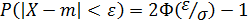(26)

Правило «трех сигм»

Пусть, например ε = 3σ. Используя таблицы функции стандартного нормального распределения найдем:

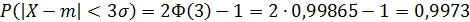
поэтому вероятность того, что случайная величина отклонится от математического ожидания больше, чем на Зσ, ничтожно мала:

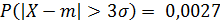
Такое событие практически невозможно. В связи с этим на практике часто используется так называемое правило «трех сигм»: отклонение нормально распределенной случайной величины от ее математического ожидания, как правило, не превышает утроенного стандартного отклонения.

Рассмотрим применение свойств нормального распределения

Пример.1 На станке-автомате изготавливаются валики номинальным диаметром 10 мм. Стандартное отклонение, характеризующее точность станка, составляет σ = 0,03 мм. Сколько в среднем валиков из ста удовлетворяют стандарту, если для этого требуется, чтобы диаметр отклонялся от номинального не более чем на 0,05 мм?

Дата добавления: 2014-01-03