С помощью критерия Колмогорова

Оценка соответствия нормальному распределению

При использовании λ-критерия (критерия А. Н. Колмогорова) предполагается, что теоретическая функция распределения непрерывна, а эмпирическая представлена несгруппированными данными. На практике для упрощения вычислений приходится группировать значения случайной величины на небольших интер­валах.

λ - критерий можно применять, когда для гипотетического pacпpeделения полностью известны из каких-либо теоретических соображений не только вид функции распределения, но и входящие в нее параметры. Чаще всего, однако, бывает известен вид функции, параметры определяются из опыта. При использовании критерия это обстоятельство учитывают, уменьшая число степеней свободы. Критерий λ такой поправки не предусматривает, в связи с чем eго применение в большинстве случаев приводит к завышенному согласию, если параметры теоретического распределения заранее не известны.

План расчета критерия λ:

1. Сначала находят разницу между максимальной и минимальной величинами, т.е. размах варьирования по формуле (6).

2. Определяют классовый интервал

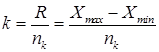
где n_k - число классов, 7<m<20.

Желательно, чтобы величина k была кратной 5 или 10.

3. Разбивают полученные значения на классы, которые располагаю по возрастанию значений, и результаты представляют в таблице.

Напротив наибольшего числа значений в классе отмечают условное отклонение 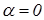, от него увеличивающиеся на единицу отклонения: вниз – положительные, вверх – отрицательные.

4.Среднее значение выборки определяют по формуле:

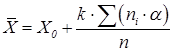
где Х – среднее значение в классе при a = 0;

k – классовый интервал;

n – общее число измерений.

5. Среднее квадратическое отклонение

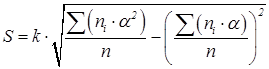
6. Составляем итоговая таблицу для расчета критерия Колмогорова (таблица 10).

7. Вычисляем эмпирические частости 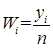, а также их на­копленные значения Σ W_i. Значения Σ W_i вычисляются путем сложения величин W_i таким образом, что для каждого последующего класса оно будет равно сумме значений W_i предыдущих классов. Таким образом, для последнего класса Σ W_i =1.

8. Значения накопленных теоретических частостей Σ W определяют по величине 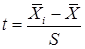для нормального распределения (таблица 11).

9. Далее по каждой строке расчетной таблицы вычисляют абсолютные значения разностей 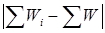и обозначают максимальную из них через D_m.

Таблица 10

Границы классов

Среднее значение в классе

Число значений в классе (частота попадания в класс) yi

Условное отклонение a

yi a

yi a^2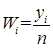

Σ Wi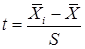

Σ W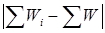

Таблица 11

t	Σ W	t	Σ W	t	Σ W	t	Σ W
- 3,1 -3,0 -2,9 -2,8 -2,7 -2,6 -2,5 -2,4 -2,3 -2,2 -2,1 -2,0 -1,9 -1,8 -1,7 -1,6	0,001 0,055	-1,5 -1,4 -1,3 -1,2 -1,1 -1,0 -0,9 -0,8 -0,7 -0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0,0	0,067 0,500	0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5	0,500 0,933	1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2.5 2,6 2,7 2,8 2,9 3,0 3,1	0,945 0,999

10. Критерий λ основан на максимальной величине расхождения D_m, между накопленными частостями эмпирического и теоретического распределения:

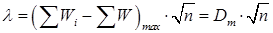(33)

где n — число испытаний.

Вероятности Р (λ) того, что критерий достигнет величины λ приведены в таблице 12.

Таблица 12

λ	Р(λ)	λ	Р(λ)	λ	Р(λ)	Р(λ)	Р(λ)
0,3 0,4 0,5 0,6 0,7 0,8	0,999 0,997 0,964 0,864 0,711 0,544	0,9 1,0 1,1 1,2 1,3 1,36	0,393 0,270 0,178 0,112 0,068 0,050	1,4 1,5 1,6 1,7 1,8 1,9	0,040 0,022 0,012 0,006 0,003 0,002	2,0 2,1 2,2 2,3 2,4 2,5	0,0007 0,0003 0,0001 0,0001 0,0000 0,0000

11. Если Р(λ) < q =0,05, следовательно гипотеза о соответствии результатов испытаний нормальному закону распределения отвергается.

Если λ попадет в критическую область, т. е. если Р(λ) окажется меньше уровня значимости q, то это свидетельствует о малой вероятности такого большого значения критерия λ в условиях выдвинутой нулевойгипотезы, т. е. о неправильности гипотезы согласия, нужно искать другой теоретический закон распределения и повторить проверку гипотезы близости к нему эмпирического распределения.

В программе Excel не предусмотрен расчет критерия Колмогорова с помощью встроенных функций.

Дата добавления: 2014-01-03