С помощью критерия Пирсона

Оценка соответствия нормальному распределению

Этот метод используется для проверки согласия опытного и теоретического распределения, если число испытаний больше 100.

Суть метода заключается в определении критерия Пирсона (c²) с последующим сравнением полученного значения с теоретическим.

Порядок определения критерия Пирсона:

Определяют среднее значение и среднее квадратическое отклонение. Для расчета критерия Пирсона составляют таблицу (таблица 13).

2. Определяют отношение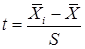

3. С помощью специальной таблицы (таблица 14) определяют частоту распределения Y₀.

4. Рассчитывают теоретическое значение частот

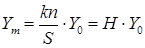(34)

где n - общее число испытаний;

k - классовый интервал;

S - среднее квадратическое отклонение.

5. Определяют разность между фактической и теоретической частотой распределения

y_i – U_т (35)

рассчитывают

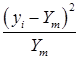(36)

6. Находят критерий Пирсона

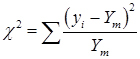(37)

7. Определяют число степеней свободы

С = m-3 (38)

где C - число степеней свободы;

m - число классов или строк.

8. Задаваясь доверительной вероятностью q, определяют теоретическое значение критерия Пирсона.

Таблица 13

Границы классов	Среднее значение в классе	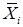Число значений в классе (частота попадания в класс) yi	Условное отклонение a	yi a	yi a^2		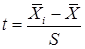Y0	Теоретические частоты

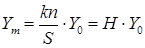
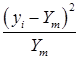
Таблица 14

t	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9	0,3989 0,2420 0,0544 0,0044

9. Сравнивают c_ф² с c_т^2. Если c²_ф < c²_т, то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределения принимается, в противном случае отвергается.

В программе Excel проверка осуществляется с помощью функции ХИ2ТЕСТ (рис. 32). ХИ2ТЕСТ возвращает значение для распределения χ² Критерий используется для определения того, подтверждается ли гипотеза экспериментом.

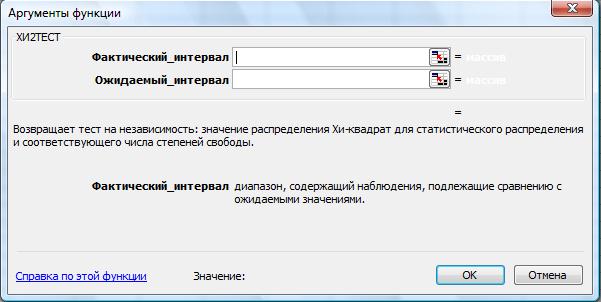
Рис. 32. Функция ХИ2ТЕСТ

ХИ2ТЕСТ (фактический_интервал; ожидаемый_интервал)

Фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями.

Ожидаемый_интервал — это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.

Если фактический_интервал и ожидаемый_интервал имеют различное количество точек данных, то функция ХИ2ТЕСТ возвращает значение ошибки #Н/Д.

Критерий χ² сначала вычисляет χ² статистику, используя формулу:

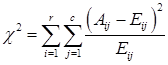(39)

где A_ij - фактическая частота в i -ой строке, j -ом столбце

E_ij - ожидаемая частота в i-ой строке, j-ом столбце

r - число строк

c - число столбцов

Значение критерия χ² является индикатором независимости. Как видно из формулы, критерий χ² всегда положительный или равен 0, а последнее возможно только, если A_ij = E_ij при любых значениях i,j.

ХИ2ТЕСТ возвращает вероятность того, что при условии независимости может быть получено значение χ² статистики по крайней мере такое же высокое, как полученное из приведенной выше формулы. Чтобы вычислить эту вероятность, ХИ2ТЕСТ использует распределение χ² с соответствующим числом степеней свободы (df). Если r > 1, а c > 1, то df = (r - 1)(c - 1). Если r = 1, а c > 1, то df = c - 1 или если r > 1, а c = 1, то df = r - 1. Равенство, где r = c= 1, не позволительно, поэтому появится сообщение об ошибке #Н/Д.

Функцию ХИ2ТЕСТ можно использовать в тех случаях, когда гипотетическое распределение задано полностью, то есть заданы не только вид гипотетического закона распределения, но и все параметры этого закона. Только в этом случае функция правильно выдает число степеней свободы.

ХИ2РАСП (x;степени_свободы) (рис. 33) возвращает одностороннюю вероятность распределения хи-квадрат. Распределение χ² связано с критерием χ². Критерий χ² используется для сравнения предполагаемых и наблюдаемых значений. Например, в генетическом эксперименте выдвигается гипотеза, что следующее поколение растений будет обладать определенной окраской. Сравнивая наблюдаемые результаты с предполагаемыми, можно определить, была ли верна исходная гипотеза.

х – значение, для которого требуется вычислить распределение.

Степени_свободы – число степеней свободы.

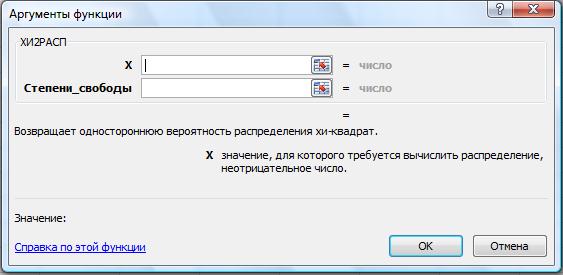
Рис. 33. Функция ХИ2РАСП

Если какой-либо из аргументов не является числом, функция ХИ2РАСП возвращает значение ошибки #ЗНАЧ!.

Если x отрицательное значение, функция ХИ2РАСП возвращает значение ошибки #ЧИСЛО!

Если значение аргумента «степени_свободы» не является целым числом, оно усекается.

Если степени_свободы < 1 или степени_свободы > 10^10, функция ХИ2РАСП возвращает значение ошибки #ЧИСЛО!.

ХИ2РАСП вычисляется как ХИ2РАСП = P(X> x), где x — χ² случайная величина.

ХИ2ОБР (вероятность;степени_свободы) (рис. 34) возвращает значение, обратное односторонней вероятности распределения хи-квадрат. Если вероятность = ХИ2РАСП (x;...), то ХИ2ОБР (вероятность;...) = x. Данная функция позволяет сравнить наблюдаемые результаты с ожидаемыми, чтобы определить, была ли верна исходная гипотеза.

Вероятность — вероятность, связанная с распределением c2 (хи-квадрат).

Степени_свободы — число степеней свободы.

Если какой-либо из аргументов не является числом, функция ХИ2ОБР возвращает значение ошибки #ЗНАЧ!

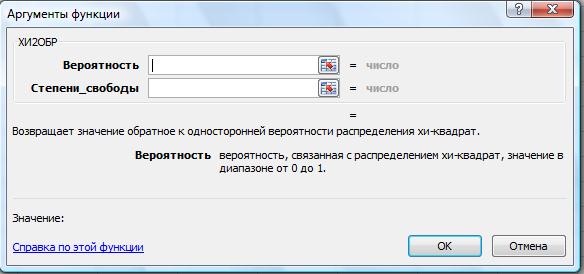
Рис. 34. Функция ХИ2ОБР

Если вероятность < 0 или вероятность > 1, функция ХИ2ОБР возвращает значение ошибки #ЧИСЛО!

Если значение аргумента «степени_свободы» не является целым числом, оно усекается.

Если степени_свободы < 1 или степени_свободы ≥ 10^10, ХИ2ОБР возвращает значение ошибки #ЧИСЛО!

Если задано значение вероятности, то функция ХИ2ОБР ищет значение x, для которого функция ХИ2РАСП (x; степень_свободы) = вероятность. Однако точность функции ХИ2ОБР зависит от точности ХИ2РАСП. В функции ХИ2ОБР для поиска применяется метод итераций. Если поиск не закончился после 100 итераций, функция возвращает сообщение об ошибке #Н/Д.

Дата добавления: 2014-01-03