Сравнение двух дисперсий независимых выборок

(критерий Фишера)

Для сравнения дисперсий двух выборок применяется критерий Фишера. Он определяется по следующей формуле

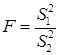(50)

где 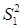- наибольшая дисперсия;

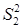- наименьшая дисперсия.

Далее расчетный критерий сравнивается с табличным значением. Если F>F_расч, то гипотеза о равенстве дисперсий отвергается.

Значения критерия Фишера (F-критерия) для уровня значимости p = 0,05 приведены в таблице 17, где f₁ - число степеней свободы большей дисперсии, f₂ - число степеней свободы меньшей дисперсии.

В программе Excel проверка однородности дисперсий осуществляется с помощью функции ФТЕСТ (рис. 40). F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, то можно определить, имеют ли эти школы различные уровни разнородности учащихся по результатам тестирования.

Таблица 17

	f1
f2
	161,45	199,50	215,71	224,58	230,16	233,99	236,77	238,88	240,54	241,88	245,95
	18,51	19,00	19,16	19,25	19,30	19,33	19,35	19,37	19,38	19,40	19,43
	10,13	9,55	9,28	9,12	9,01	8,94	8,89	8,85	8,81	8,79	8,70
	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96	5,86
	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,77	4,74	4,62
	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06	3,94
	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,64	3,51
	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,35	3,22
	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,14	3,01
	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,98	2,85
	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,85	2,72
	4,75	3,89	3,49	3,26	3,11	3,00	2,91	2,85	2,80	2,75	2,62
	4,67	3,81	3,41	3,18	3,03	2,92	2,83	2,77	2,71	2,67	2,53
	4,60	3,74	3,34	3,11	2,96	2,85	2,76	2,70	2,65	2,60	2,46
	4,54	3,68	3,29	3,06	2,90	2,79	2,71	2,64	2,59	2,54	2,40
	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,49	2,35
	4,45	3,59	3,20	2,96	2,81	2,70	2,61	2,55	2,49	2,45	2,31
	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,46	2,41	2,27
	4,38	3,52	3,13	2,90	2,74	2,63	2,54	2,48	2,42	2,38	2,23
	4,35	3,49	3,10	2,87	2,71	2,60	2,51	2,45	2,39	2,35	2,20

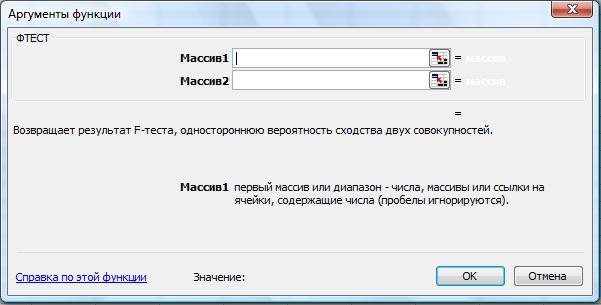
Рис. 40. Функция ФТЕСТ

ФТЕСТ (массив1; массив2)

Массив1— это первый массив или интервал данных.

Массив2— это второй массив или интервал данных.

Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

Если количество точек данных в аргументе массив1 или массив2 меньше 2, или если дисперсия аргумента массив1 или массив2 равна нулю, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!.

В надстройке «Пакет анализа» используется двухвыборочный F-тест для дисперсии.

Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» приведены на рис. 41. Элементы диалогового окна «Двухвыборочный F-тест для дисперсии» совпадают с элементами диалогового окна «Двухвыборочный t-тест с одинаковыми дисперсиями».

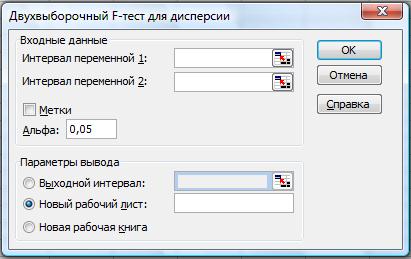
Рис. 41. Двухвыборочный F-тест для дисперсии

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.

Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.

С помощью этого средства вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, "P(F <= f) одностороннее” дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости Alpha. Если f > 1, “P(F <= f) одностороннее” дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение большее 1 для Alpha.

Дата добавления: 2014-01-03