Ранг матрицы

Пусть дана матрица размерности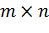

.

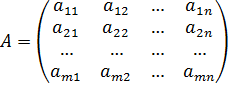Выделим в ней 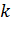строк и 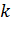столбцов. 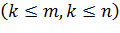. Из элементов, стоящих на пересечении 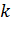строк и 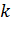столбцов составим определитель 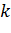– го порядка. Все такие определители называют минорами матрицы.

Пример 26. Для матрицы 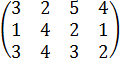минорами второго порядка будут, например, определители

, , , , , , , , .

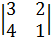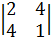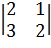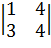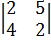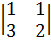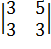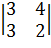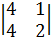Минорами третьего порядка - , , , .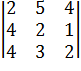

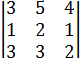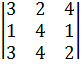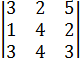Всего для матрицы 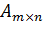можно составить 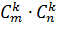миноров порядка 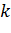, где 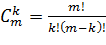. Так для матрицы 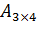существует всего

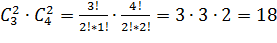миноров второго порядка.

Наибольший из порядков минора данной матрицы, отличных от нуля называется рангом матрицы. Обозначаются как .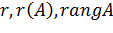

Минор, порядок которого равен рангу матрицы, называют базисным минором. У каждой матрицы может быть несколько базисных миноров.

Свойства ранга матрицы.

1. При транспонировании матрицы её ранг не меняется.

2. Если из матрицы убрать нулевую строку (нулевой столбец), то ранг матрицы не изменится.

3. Ранг матрицы не меняется при её элементарных преобразованиях.

4. Ранг матрицы равен числу не нулевых строк в её ступенчатом виде.

Дата добавления: 2014-01-03