Двойной интеграл, его свойства и вычисление

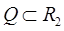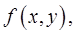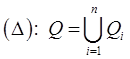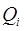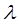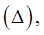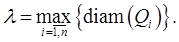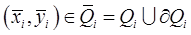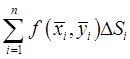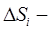Пусть даны – замкнутая ограниченная область (компакт) и функция определенная в этой области. Произведем разбиение этой области на частичные подобласти с помощью конечного числа непрерывных кривых. Обозначим через диаметр разбиения т.е. число Возьмём произвольно точку и составим интегральную сумму (где площадь области ).

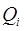Определение 1. Если существует конечный предел интегральных сумм: 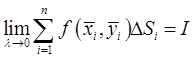и если этот предел не зависит от вида разбиения 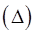и выбора точек 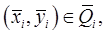то его называют двойным интегралом от функции 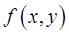по области и обозначают

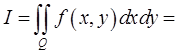
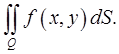
При этом функция 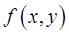называется интегрируемой по области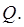

Отметим без доказательства следующие свойства:

1) Любая функция, непрерывная на компакте , интегрируема на этом компакте;

2) Если функция ограничена на компакте и имеет на нем разрывы разве что на конечном числе непрерывных кривых, то она интгрирума в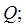

3) Двойной интеграл от произвольной ограниченной функци по ограничен-

ной кусочно непрерывной кривой равен нулю.

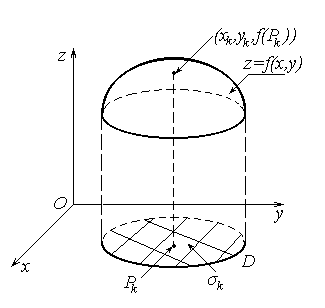
Геометрический смысл двойного интеграла. Рассмотрим цилиндрическое тело 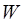с нижним основанием , верхним основанием - поверхностью 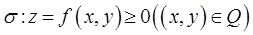и с образующей боковой поверхности, параллельной оси 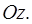Произведение 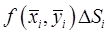есть объём цилиндра высоты 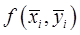и площадью основания 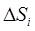, а интегральная сумма 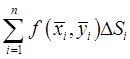– суть объём ступенчатого тела, построенного по разбиению 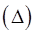. Ясно, что обём тела 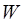приближенно равен объёму этого ступенчатого тела, т.е. 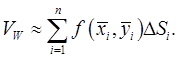Это равенство будет тем точнее, чем мельче разбиение 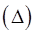, и при 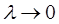оно становится точным, т.е.

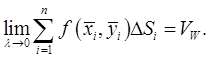Здесь слева стоит двойной интеграл 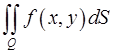, поэтому 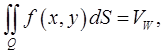т.е. двойной интеграл 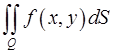равен объёму цилиндрического тела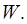

Двойные интегралы обладают свойствами, аналогичными свойствам одномерных интегралов. Сформулируем их, предполагая, что 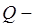замкнутая ограниченная квадрируемая область в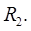

1⁰) (линейность ) Если функции 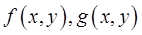интегрируемы в , то и любая их линейная комбинация 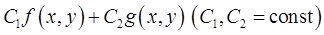также интегрируема в , причем имеет место равенство

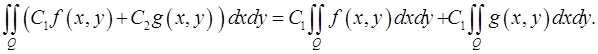
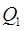2⁰) (аддитивность) Если область разбита на две непересекающиеся подобласти и 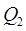с помощью непрерывной кривой и если функция 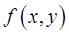интегрируема в , то она интегрируема и в каждой из областе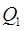й и 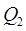(и наоборот). При этом имеет место равенство

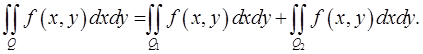
3⁰) (монотонность) Если функции 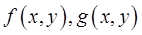интегрируемы в и имеет место неравенств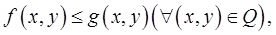о то

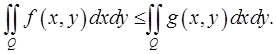
4⁰) Если функция 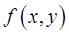интегрируема в и имеют место неравенства

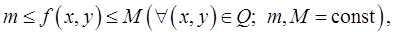
то

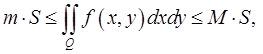
где 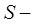площадь области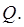

5⁰) (теорема о среднем) Если функция 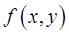непрерывна в замкнутой ограниченной области 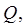то существует точка 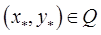такая, что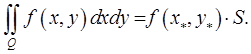

Геометрически это означает, что если 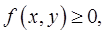то объём цилиндрического тела 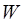с верхним основанием 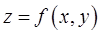и с нижним основанием равен объёму некоторогоого параллелепипеда с тем же основанием и высотой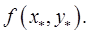

При вычислении двойных интегралов используются повторные интегралы, которые имеют следующий смысл:

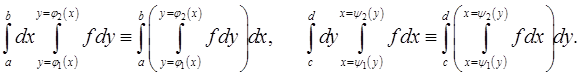
Теорема 1 (Фубини). Если 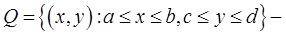прямоугольник и если функция 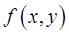кусочно непрерывна в то

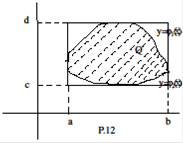
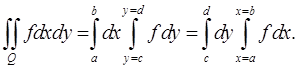
Теорема 2 (вычисление двойного интеграла в криволинейной области). Если имеет вид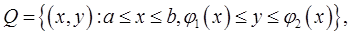

где функции 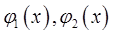непрерывны на отрезке 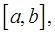и если функция 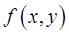непрерывна в 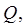то

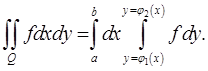
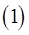
Доказательство. Обозначим 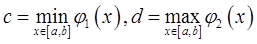, 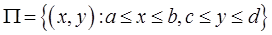и рассмотрим функцию

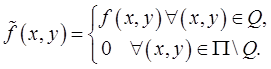
Эта функция кусочно непрерывна в 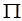, поэтому применима теорема Фубини:

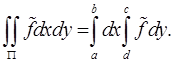
Так как

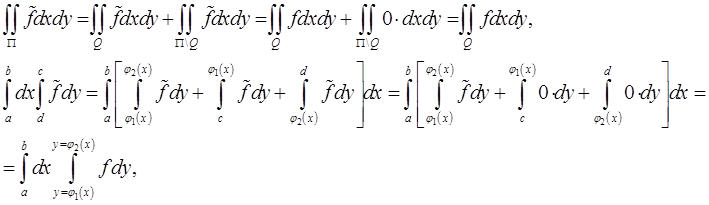
то 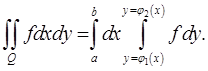Теорема доказана.

Замечание 1. В случае области типа

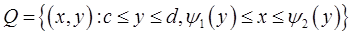
и непрерывности функции 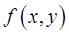и функций 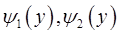имеет место равенство

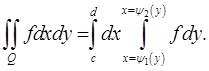
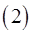
Заметим, что области 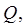которые участвуют в формулах (1) и (2), являются правильными областями. Более точно: область называется правильной в направлении оси 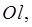если любая прямая, параллельная оси 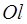, пересекает границу области не более чем в двух точках. Если область – неправильная, то её разбивают на правильные подобласти с помощью конечного числа непрерывных кривых и применяют к соответствующему интегралу теорему об аддитивности интеграла.

Замечание 2. Если область является правильной как в направлении оси 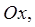так и в направлении оси 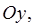то имеет место равенство

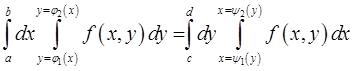
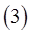
(в предположении, что все участвующие здесь функции непрерывны в соответствующих областях). Таким образом, в случае области описанного типа можно изменять порядок интегрирования. Этим часто пользуются, желая упростить вычисление двойного интеграла.

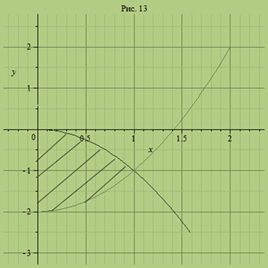Пример 1( Кузнецов Л.А. Типовые расчеты ). Изменить порядок интег-рирования

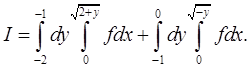
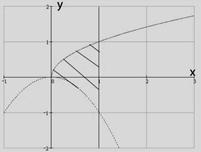
Решение. Сначала нарисуем область , по которой берется соответствующий двойной интеграл. Она находится между двумя параболам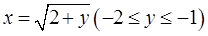и и 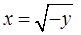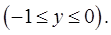Изменяя порядок интегрирования, найдём, что 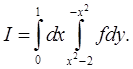Поясним, как получен этот результат. Спроектируем область на ось 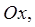получим отрезок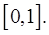Значит, пределы внешнего интеграла – суть числа 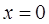и 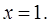Теперь зафиксируем произвольно 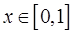и проведем через точку 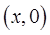луч в направлении оси 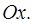Он пересечет нижнюю границу области в точке с ординатой 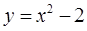(это будет нижняя граница внутреннего интеграла), а верхнюю границу области 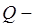в точке с ординатой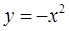 (это будет верхняя граница внутреннего интеграла).

Пример 2 ( Кузнецов Л.А. Типовые расчеты ). Вычислить интеграл

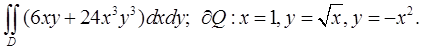
Дата добавления: 2014-01-03