Тройной интеграл, его свойства и вычисление

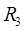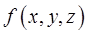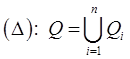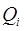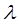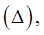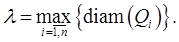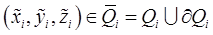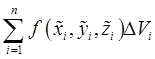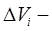Пусть – замкнутая ограниченная (кубируемая) область (тело) в и функция определена в . Произведем разбиение этой области на частичные подобласти с помощью конечного числа непрерывных поверхностей. Обозначим через диаметр разбиения т.е. число Возьмём произвольно точку и составим интегральную сумму (где объём области ).

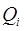Определение 2. Если существует конечный предел интегральных сумм: 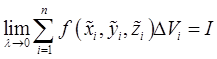и если этот предел не зависит от вида разбиения 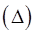и выбора точек 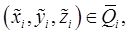то его называют двойным интегралом от функции 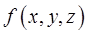по области и обозначают 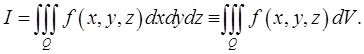При этом функция 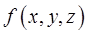называется интегрируемой в области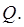

Механический смысл тройного интеграла. Если 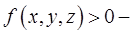плотность тела в точке 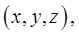то произведение 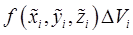приближенно равно массе тела 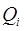, а интегральная сумма 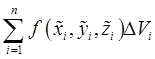приближенно равна массе всего тела 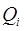, т.е. 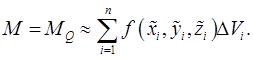Ясно, что это равенство будет тем точнее, чем мельче разбиение 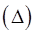, и при 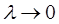оно становится точным:

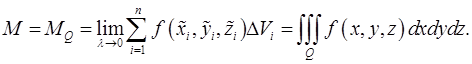
Таким образом, тройной интеграл по телу от плотности 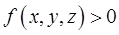равен массе тела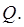

Тройные интегралы обладают свойствами, аналогичными свойствам двойных интегралов. Сформулируем их, предполагая, что 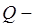замкнутая ограниченная кубируемая область в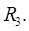

1⁰) (линейность ) Если функции 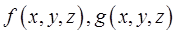интегрируемы в , то и любая их линейная комбинация

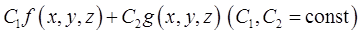
также интегрируема в , причем имеет место равенство

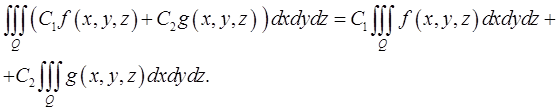
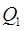2⁰) (аддитивность) Если область разбита на две непересекающиеся подобласти и 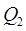с помощью непрерывной поверхности и если функция 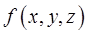интегрируема в , то она интегрируема и в каждой из областе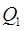й и 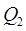(и наоборот). При этом имеет место равенство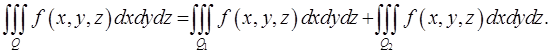

3⁰) (монотонность) Если функции 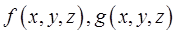интегрируемы в и имеет место неравенств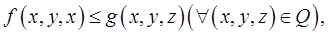о то

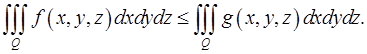
4⁰) Если функция 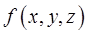интегрируема в и имеют место неравенства

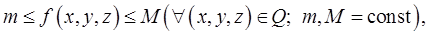
то

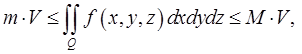
где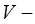объём области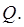

5⁰) (теорема о среднем) Если функция 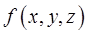непрерывна в замкнутой ограниченной области 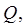то существует точка 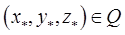такая, что

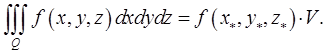
И, наконец, отметим, что любая непрерывная и кусочно непрерывная в замкнутой ограниченной (кубируемой) области функция интегрируема в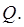

Теорема 3 (Фубини). Если

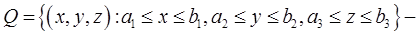
параллелепипед и если функция 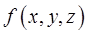кусочно непрерывна в 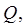то

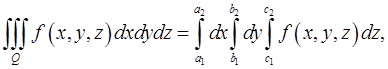
причем здесь порядок интегрирования может быть изменён как-угодно.

Теорема 4 (вычисление тройного интеграла в криволинейной области). Если имеет вид

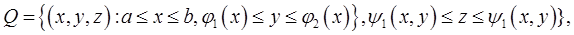
где функции 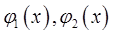непрерывны на отрезке 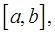а функции 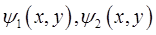непрерывны в области 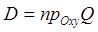и если функция 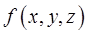непрерывна в 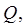то

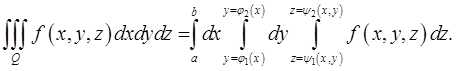
Доказательство этой теоремы фактически повторяет доказательство теоремы 2 и опирается на теорему Фубини. Заметим, что если область является правильной в направлении всех трех осей, то можно изменять порядок интегрирования.

Пример 4 ( Кузнецов Л.А. Типовые расчеты ). Вычислить интеграл 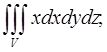где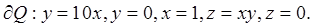

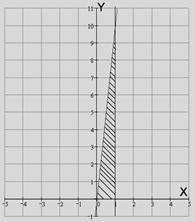Решение. Нарисуем проекцию 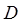области на плоскость 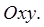Границу 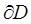образуют прямые 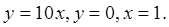Сначала расставим пределы по 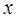и 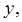используя область 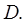Затем возьмем произвольно точку 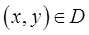и проведем через неё луч в направлении оси 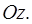Она пересечет нижнюю границу области в точке 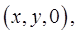а верхнюю границу этой области – в точке 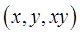. Значит, нижний предел интеграла по 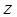будет 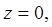а верхний предел по 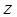будет В результате получим

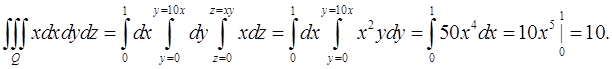
Дата добавления: 2014-01-03