Генеральная и выборочная совокупности

Текст лекции

Лекция 14 Генеральная и выборочная совокупности

Учебные и воспитательные цели:

1. Дать представление о генеральной и выборочной совокупности.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия
II. Основная часть занятия
Введение в лекцию	5-10
1. Генеральная и выборочная совокупности
Заключение по лекции
III. Заключительная часть занятия

Введение в лекцию:

В материалах сегодняшней лекции мы рассмотрим генеральную и выборочную совокупности.

Учебные вопросы лекции:

Математическая статистика занимается сбором, анализом и обработкой данных наблюдений. Эти данные относятся к массовым явлениям, на которые влияют случайные факторы.

Статистические методы используются для контроля массового производства, в области физики, в астрономии, экономике, биологии и т.п. Рассмотрим три основные задачи математической статистики:

1) упорядочение статистического материала, статистические законы распределения;

2) статистическое оценивание характеристик распределения;

3) статистическая проверка гипотез.

1.1. Статистическое описание резул ьтатов наблюдений

При изучении качественного или количественного признака, характеризующего совокупность однородных объектов, не всегда имеется возможность обследовать каждый объект изучаемой совокупности. Приведём такой пример. Электрическую лампочку условимся считать стандартной, если продолжительность её горения не менее 1200 ч, в противном случае она считается нестандартной. За качеством продукции обязан следить завод-изготовитель. Исследовать каждую лампочку на продолжительность горения практически невозможно, да это и противоречит здравому смыслу. Как же получить представление о качестве изготовляемой продукции? Пусть заводу необходимо поставить потребителю партию готовых изделий. Вместо данных о качестве всех электрических лампочек партии достаточно получить точные сведения о качестве небольшой их части, отобранных случайно. По продолжительности горения отобранных лампочек можно судить о качестве всех лампочек партии. Практика подтверждает, что сделанные выводы бывают достаточно надёжными.

Совокупность всех возможных, иногда говорят, – всех мыслимых, значений исследуемой случайной величины называют генеральной совокупностью.

Множество значений случайной величины, полученное в результате наблюдений над нею, называют случайной выборкой или просто выборкой.

Число объектов в генеральной совокупности и в выборке называют их объёмами. Генеральная совокупность может иметь как конечный, так и бесконечный объём.

Рассмотрим наблюдение за некоторым измеряемым признаком какого либо объекта, например, возраст людей, сортность изделий и др.

Значение признака генеральной совокупности – это: случайная величина X, связанная с испытанием (наблюдением). Эта случайная величина распределена по некоторому закону с неизвестными параметрами, который называется распределением генеральной совокупности.

Проведём п испытаний при одних и тех же условиях. Случайная ве­личина X принимает значения .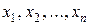

Это множество значений называется выборкой объёма п.

Элементы выборки, записанные в порядке их регистрации, труднообозримы и неудобны для дальнейшего анализа. Необходимо получить такое описание выборки, которое позволяет выделить характерные особенности исходных данных, Для этого существуют различные способы группировки данных выборки.

Пусть выборка объёма n содержит m различных чисел. Изменив нумерацию, запишем их в виде ,

причём 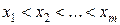. Число т называется размахом выборки.

Пусть значение 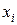встречается в выборке раз, 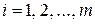. Число называется абсолютной частотой, а число - относительной частотой элемента .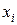

Таблица

Х			…
			…

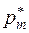
называется статистическим рядом.

При большом объёме выборки используется группированный статистический ряд. Для этого все элементы выборки распределяются по группам или интервалам группировки. Интервал, содержащий все элементы выборки, разбивается на k непересекающихся интервалов , не обязательно равных по длине.

Если - число элементов выборки, попавших в интервал , а 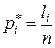их частота, то можно составить таблицу

Номер	Границы	Частоты	Относительные
интервала	интервала		частоты
…	…	…	…
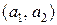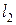k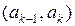

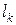
Эта таблица называется группированным статистическим рядом. Если наблюдаемое значение попадает на границу соседних интервалов, то число его наблюдений относят к правому интервалу.

По данным выборки можно построить статистическую функцию распределения .

Для наглядного представления выборки используют гистограмму и полигон частот.

Гистограмма относительных частот строится по группированному

статистическому ряду. Для этого находится 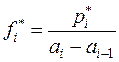(статистическая плотность) .

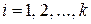Гистограмма - это ступенчатая фигура, состоящая из прямоугольников с основаниями и высотами 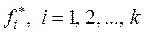(рис. 1).

При увеличении объёма выборки и уменьшении интервала группировки гистограмма относительных частот является статистическим аналогом плотности распределения генеральной совокупности.

Полигон относительных частот - это ломаная линия с вершинами , взятыми из статистического ряда (рис. 2).

Заключение по лекции:

В лекции мы рассмотрели генеральную и выборочную совокупности. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Задание на самостоятельную работу

Изучить:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил. стр 191-200.

Дата добавления: 2014-01-03