Многомерный регрессионный анализ

В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак Y, а независимые признаки 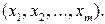Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом: Y - независимые случайные величины со средним 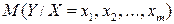и постоянной дисперсией 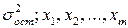— линейно независимые векторы 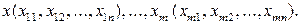Все положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида

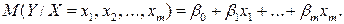(2.13)

Оценке подлежат параметры 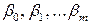и остаточная дисперсия. Заменив параметры их оценками, запишем уравнение регрессии

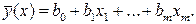(2.14)

Коэффициенты в этом выражении находят методом наименьших квадратов.

Исходными данными для вычисления коэффициентов является выборка из многомерной совокупности, представляемая обычно в виде матрицы X и вектора Y:

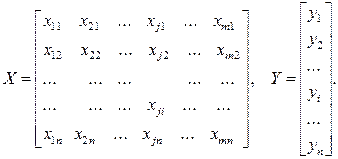
Как и в двумерном случае, составляют систему нормальных уравнений

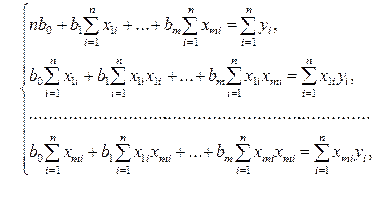(2.15)

которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение b _o через остальные параметры:

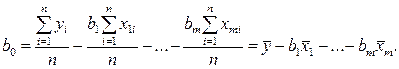(2.16)

Подставим в остальные уравнения системы вместо b _o полученное выражение:

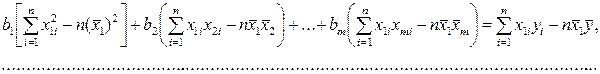
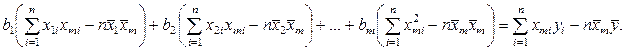Пусть С — матрица коэффициентов при неизвестных параметрах 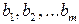; 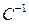— матрица, обратная матрице С; 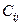— элемент, стоящий на пересечении i -й строки и i -го столбца матрицы 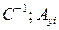— выражение 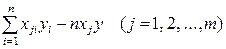. Тогда, используя формулы линейной алгебры, запишем окончательные выражения для параметров:

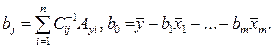(2.17)

Оценкой остаточной дисперсии 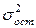является

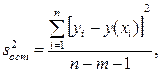
где 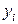— измеренное значение результативного признака; 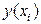значение результативного признака, вычисленное по уравнению регрессий.

Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику 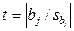вычисляют для каждого j -го коэффициента регрессии 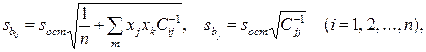(2.18)

где 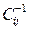—элемент обратной матрицы, стоящий на пересечении i -й строки и j -го столбца; 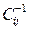— диагональный элемент обратной матрицы.

При заданном уровне значимости α и числе степеней свободы k=n—т— 1 по табл. 1 приложений находят критическое значение 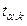. Если 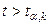, то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если 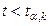, то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.

Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: 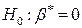(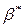— вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики 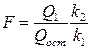, где Q ₁ — сумма квадратов, характеризующая влияние признаков Х; Q _ocт — остаточная сумма квадратов, характеризующая влияние неучтённых факторов; k₂=n—m—1, k₁=m. Для уровня значимости α и числа степеней свободы k ₁ и k ₂ по табл. 3 приложений находят критическое значение 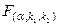. Если 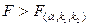, то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. При 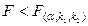нет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.

Дата добавления: 2014-01-03