Лекция №7

Беттер. Қырлы беттер. Түзу сызықты беттер.

Өзара қиылысатын жазықтардан құралған беттерді қырлы беттер дейді.

S₁

Жазықтықтардың қиылысу сызықтары көпжақтардың қабырғалары, ал барлық жақтардың ортақ нүктесі (бірнеше жазықтықтардың қиылысу нүктесі) қырлы беттердің төбесі деп аталады. Сызбада қырлы беттер олардың қабырғаларының толық берілуімен анықталады. Мысалы, 1 суретте үшқырлы пирамида а, b және с қабырғаларымен берілген, S нүктесі беттің төбесі 2 суретте қабырғалары бір-біріне параллель m, n және k түзулерімен берілген призма көрсетілген.

    Сурет 1

    Сурет 2

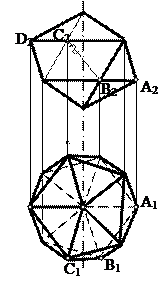
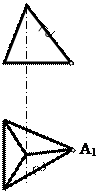
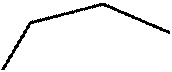
Қырлы беттер өздерінің S төбесімен және кейбір жазық немесе кеңіс сынық – а сызығымен берілуі мүмкін. Бұл жағдайда а сынық сызығы қырлы беттің бағыттаушысы болады. Призмалық беттер үшін S төбесі 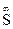нүктесінің (сурет 4) өзіндік емес нүктесі болады және кеңістікте бағытымен беріледі.

S1 S2 a1 a2
Сурет 3	Сурет 4

Беттерді құрайтын жазықтықтар кеңістікті барлық жағынан тұйықтайтын болса, қырлы беттерді көпжақтар деп атайды. Көпжақтар өздерінің жақтарымен, қабырғаларымен және төбелерімен сипатталады.

Егер көпжақтың барлық элементтері оның кез-келген жағының бір жазықтығында орналасқан болса, онда көпжақ дөңес деп аталады.

		D1
	A1

E₁

C₁

F₁

B₁

B₂

F₂

D₂

C₂

E₂

А₂

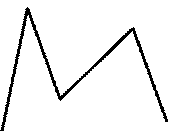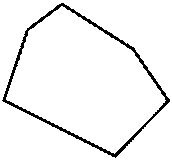
Дөңес көпжақтың жақтары дөңес көпбұрыштар болады. Егер көпжақтың барлық қабырғалары, жақтары, екіқырлы және кеңіс бұрыштары бір-бірімен тең болса, онда ондай көпжақтар дұрыс дөңес көпжақтар (Платон денесі) деп аталады. Дұрыс көпжақтардың бес түрі бар: – тетраэдр (төртжақ), жақтары төрт теңжақты үшбұрыштар болады (сурет 6); – октаэдр (сегізжақ), жақтары сегіз теңжақты үшбұрыштар болады (сурет 7); – икосаэдр (жиырмажақ), жақтары жиырма теңжақты үшбұрыштар (сурет 8);  

    Сурет 5  

– гексаэдр (алты жақ) – жақтары алты квадрат болатын куб (сурет 9);

– додекаэдр (он екі жақ), жақтары он екі дұрыс бесбұрыш (сурет 10).

Дұрыс көпжақтардың барлығына сырттай сфера жүргізуге болады.

Сурет 6

Сурет 7

Сурет 8

Сурет 9

Көпжақ қарапайым деп аталады, егер:

– оның барлық жақтары қарапайым көпбұрыштар болса, яғни сыбайлас емес жақтар жұбының ортақ нүктесі болмайды;

– сыбайлас емес екі жақтың ортақ нүктесі болмайды (ортақ төбесінен басқасы);

Беттерді салу үшін қажетті және жеткілікті шарттардың жиынтығын беттердің анықтаушысы деп атайды. Беттердің анықтаушысы геомет-риялық және алгоритмдік бөліктерден тұрады.

Беттер анықтаушысының геометриялық бөлігі (шартты түрде ГА) сызбада берілген геометриялық фигуралар арқылы байланысатын кеңістік сызықтарының параметрлер жиыны болып табылады.

Анықтаушының алгоритмдік бөлігі (шартты түрде АА) – беттердің жасалынуы үшін анықтаушының геометриялық бөлігін қол-дануға арналған ережелердің жиынтығы.

		Т
	m

A

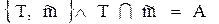Мысалы, конустық беттер үшін (сурет 10): ГА q АА q: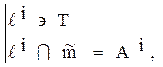 Бұл жерде Т – конустың төбесі 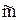- бағыттаушы қисық ℓ - жасаушы. D Î ℓ Ù ℓ Ì q Þ D Î q.

Сурет 10

Сонымен, егер эпюрде беттің геометриялық анықтаушысы берілген болса, бет моделденген деп есептелінеді.

Білім деңгейін тексеруге арналған сұрақтар

1. Беттердің жасалынуының кинематикалық әдісінің мәні неде?

2. Беттің анықтаушысы дегеніміз не?

3. Анықтаушының геометриялық және алгоритмдік бөліктерінің мағынасы қандай?

4. Бет каркасы дегеніміз не?

5. Беттер каркасының сызықтарының жасаушылар пішінінің параметрлері дегеніміз не?

6. Каркас сызығының қалыптық параметрі нені көрсетеді?

7. Бет сызбада қай кезде моделденген деп есептелінеді?

Дата добавления: 2014-01-03