
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиоматическое построение теории вероятностей
|
|
|
|
Теорема сложения вероятностей.
Теорема умножения вероятностей.
Основные законы и формулы теории вероятностей.
Условные вероятности.
Аксиоматическое построение теории вероятностей.
Лекция №2
Раздел 1. Основанные понятия и основные законы теории вероятностей.
Тема 2. Основные законы теории вероятностей.
Цель лекции: дать знания об основных законах теории вероятностей.
Вопросы лекции:
Литература:
Л1 - Бочаров П. П., Печинкин А. В. Теория вероятностей. Математическая статистика. - 2-е изд. - М.: ФИЗМАТЛИТ, 2005. - 296 с.
Л2 - Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2005. — 479 с: ил.
Л3 - Нахман А.Д., Косенкова И.В. Ряды. Теория вероятностей и математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2009.
Л4 - Плотникова С.В. Математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2005. (pdf-файл)
Чтобы аксиоматика приводила к содержательным теоретическим построениям, формально-логические определения и аксиомы должны отражать реальные понятия и отношения между ними. При этом основной задачей теории является не выяснение содержания исходных понятий, а установление связи между вероятностями различных событий или построение законов распределения случайных величин.
Применительно к теории вероятностей аксиоматический подход в современном виде был разработан академиком А.Н. Колмогоровым в 1933 году.
При аксиоматическом построении теории вероятностей, т.е. при ее формально-логическом обосновании, понятие случайного события не является первичным, а строится из более элементарных понятий. Первичным является понятие пространства элементарных событий.
Пространством элементарных событий W называется множество всех возможных взаимоисключающих исходов эксперимента. Элементы пространства W называются элементарными (простыми, неразложимыми) событиями и обозначаются буквой w. Такие события содержат только один исход.
Если W - конечное или счетное множество, то пространство элементарных событий называется дискретным и записывается в виде W= {w1, w2,…, wn} или W= {w1, w2,…, wn,…}.
Случайным событием (или просто событием) называется подмножество пространства элементарных событий; любое событие А это подмножество множества W: AÌ W.
Пусть опыт состоит в подбрасывании игральной кости. Тогда пространство элементарных событий имеет вид: W= {1, 2, 3, 4, 5, 6}= {w1, w2, w3, w4, w5, w6}.
Рассмотрим события: А - выпадение четного числа очков, В - выпадение простого числа, С - выпадение пяти очков. Эти события описываются следующими подмножествами из множества W:
A= {2, 4, 6}ÌW, B={1, 2, 3, 5}ÌW, C={5}ÌW.
В данном случае события А и В являются составными (разложимыми), так как появление этих событий эквивалентно выпадению одного из чисел, образующих подмножества А и В. Однако, событие С будет неразложимым, т.е. элементарным событием.
Из примера видно, что любое событие, связанное с данным опытом, должно распадаться на элементарные, т.е. представляться в виде суммы некоторого множества элементарных событий.
Рассмотрим еще пример. Пусть в урне имеется четыре шара, пронумерованных от 1 до 4. Из урны последовательно извлекаются два шара. Интересующее нас событие А - первый извлеченный шар нечетный, а второй - четный. Опишем пространство элементарных событий (всевозможные исходы) и событие А. В данном случае все возможные случаи описываются следующим множеством
W= {(1, 2), (1, 3), (1,4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)}.
Подмножество А имеет вид: A= {(1, 2), (1, 4), (3, 2), (3, 4)}.
Все правила включения, операции объединения, разности, пересечения совместно со всеми основными законами алгебры множеств применяются без изменений и к событиям.
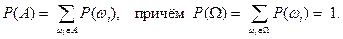
Следовательно, в случае конечного пространства W задание вероятностей элементарных событий позволяет определить вероятность любого исхода эксперимента. На практике вероятности элементарных событий определяются либо из соображений, связанных с симметрией опыта, либо на основе опытных данных.
На практике часто множество W является непрерывным. Например, при измерении координат цели, напряжения, температуры, давления и других величин пространство элементарных событий является континуумом (несчетным множеством). В таких ситуациях задать вероятность на W посредством задания вероятностей элементарных событий нельзя, так как эти вероятности не могут быть отличны от нуля. Действительно, если приписать положительные вероятности элементарным событиям, образующим несчетное множество, то сумма (несчетная) этих вероятностей может быть равна только бесконечности.
При непрерывном пространстве W ограничиваются наименьшим классом событий. В качестве событий рассматриваются только такие подмножества из W, которым можно приписать вероятность, т.е. измеримые множества. При этом требуется, чтобы система F всех таких подмножеств содержала W и была замкнута относительно операций сложения, произведения и дополнения, т.е. система F подмножеств из W, рассматриваемых в качестве событий, должна удовлетворять следующим требованиям.
1. W должно быть событием, т.е. WÎF.
2. Если в систему F входят подмножества А и B, то в нее входят также множества А+B, АВ, 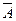 и
и 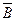 .
.
3. Если каждый элемент последовательности событий А1, А2,...,Аn,.. принадлежит системе F, то их сумма и произведение также принадлежат этой системе.
Система множеств F, удовлетворяющая условиям 1-2, называется алгеброй, а система F, удовлетворяющая условиям 1-3 - s-алгеброй.
Таким образом, в качестве событий рассматриваются только такие подмножества из W, которые образуют алгебру или s-алгебру, т.е. подмножества, принадлежащие системе F. Если W - конечное множество, то событием является любое подмножество из W, а система F всех подмножеств образует алгебру. Если W - счетное множество, то событием также является любое подмножество из W, при этом система F всех подмножеств из W образует s-алгебру. Если W -континуум (интервал или вся числовая ось), то событиями являются лишь те подмножества из W, которые принадлежат борелевской s-алгебре, т.е. совокупность множеств, образованных из интервалов с помощью конечного или счетного числа операций объединения, пересечения и взятия дополнения.
При описании дискретных или непрерывных пространств исходов иногда встречаются соответственно названия булевское поле, борелевское поле.
Аксиометрическая теория А.Н. Колмогорова основывается на четырех аксиомах, с помощью которых вводятся понятия вероятности и некоторые их свойства как для конечного множества элементарных событий, так и для любого бесконечного множества.
Аксиома 1. Каждому событию А, принадлежащему F, ставится в соответствие неотрицательное число Р(A), которое называется вероятностью события А.
Аксиома 3. (аксиома сложения вероятностей). Если А и В - несовместные события, то Р(А+B)= P(А) + Р(B).
Аксиома 4. (расширенная аксиома сложения). Если А1, А2,..., Аn,... - попарно несовместные события, то
Р(А1 + А2.+…+ Аn, + …)= P(А1) +P(А2) +...+ P(Аn)+…
Тройку (W, F, P), в которой Р удовлетворяет аксиомам 1-4, а множество F не только является алгеброй событий, но и содержит счетные суммы и произведения событий, называют вероятностным пространством.
Система аксиом 1-4 вероятностного пространства дает самую общую математическую модель случайных явлений. Аксиомы представляют абстрактные эквиваленты свойств частоты появления события при многократном повторении опыта в неизменных условиях. Аксиома 1 постулирует статистическую устойчивость частоты в длинной серии испытаний и отображает основное свойство частоты, а именно, частота случайного события есть неотрицательное число, заключенное между нулем и единицей.
Аксиома 2 постулирует достоверность появления какого-либо результата из множества возможных. На основании правила сложения частот вводятся аксиомы 3 и 4.
Таким образом, аксиомы теории вероятностей введены так, чтобы вероятность события обладала основными свойствами частоты. Только в таком случае данная теория будет хорошо согласовываться с опытом.
Из приведенных аксиом вытекает ряд следствий.
1. Вероятность невозможного события равна нулю: P(Æ)=0.
2. Для любого события А справедливо соотношение 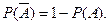
3. Каково бы ни было случайное событие А, 0£Р(А)£1.
4. Если АÌВ, то Р(А)£Р(В).
5. Если А и В - два произвольных события, то P(A+B)= P(A) + P(B) – P(AB).
6. Если А1, А2,..., Аn - произвольные события, то
P(А1 + А2 + … Аn) £ P(А1) + P(А2) +...+ P(Аn).
Аксиомы 1-4 составляют основу всей теории вероятностей. Все теоремы, правила этой теории выводятся из них формально-логическим путем. Так, например, исходя из очевидного соотношения между подмножествами 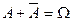 и используя аксиомы 2 и 3, получаем, что
и используя аксиомы 2 и 3, получаем, что 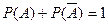 .
.
Так как Р(A) и Р(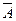 ) неотрицательные числа, то Р(A)£1.
) неотрицательные числа, то Р(A)£1.
Этот факт не содержится непосредственно ни в одной из аксиом.
В качестве другого следствия аксиом получим формулу
 |
P(A+B)= P(A) + P(B) – P(AB), (1.9.1)
где А и В - совместные события. Для этого рассмотрим следующие соотношения между событиями как между подмножествами множества W (рис.1.13):
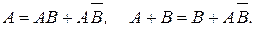
Применяя к обоим равенствам аксиому сложения, получим два числовых равенства:
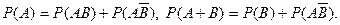
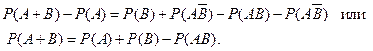 Используя выражение (1), можно получить формулу для P(A1+A2+A3). Обозначим А= А1+А2, B= А3. Тогда из (1) и формулы AB= A1A3+A2A3 следует, что
Используя выражение (1), можно получить формулу для P(A1+A2+A3). Обозначим А= А1+А2, B= А3. Тогда из (1) и формулы AB= A1A3+A2A3 следует, что
P(A1+A2+A3)= P(A1+A2) + P(A3) - P(A1A3+A2A3)= P(A1) + P(A2) - P(A1A2) + P(A3) - [P(A1A3) + P(A2A3) - P(A1A3A2A3)]= P(A1) + P(A2) + P(A3) - P(A1A2) - P(A1A3) - P(A2A3) + P(A1A2A3).
Рассмотрим несколько примеров на построение вероятностного пространства (W, F, P), которое полностью описывает случайное явление. Для этого нужно выполнить несколько операций.
Во-первых, необходимо описать пространство элементарных событий W; во-вторых, выделить класс событий F, т.е. определить систему подмножеств из W, образующих алгебру или s-алгебру; в-третьих, каждому событию АÌW, AÎF приписать вероятность таким образом, чтобы Р(W) = 1. Выбор W и выделение алгебры или s-алгебры определяются существом задачи и природой множества W.
Пример 1.9.1. Пусть подбрасывается один раз игральная кость и требуется сформировать вероятностное пространство. Из условия видно, что W = {1, 2, 3, 4, 5, 6}= {w1, w2, w3, w4, w5, w6}. Алгебра F состоит из всех подмножеств из W, число которых равно 26= 64. В силу симметрии опыта, вероятности элементарных событий Р(wi)= 1/6, причём 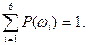 Тогда вероятность любого события А = {wi1, wi2, wi3, wi4, wi5, wiк}, wijÎW, AÎ F можно определить так
Тогда вероятность любого события А = {wi1, wi2, wi3, wi4, wi5, wiк}, wijÎW, AÎ F можно определить так
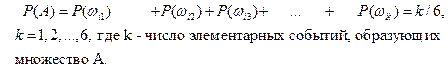
В данном случае вероятностное пространство образуют множества W= {w1, w2, w3,, w4, w5, w6}, алгебрa F= {Æ, {1}, {2},…,{6 }, {1, 2 },...,W} и числовая функция Р(A)= k/6, определенная на системе событий F.
В заключение подведем некоторые итоги.
1. Аксиоматическое построение теории вероятностей это формально-логическое ее обоснование.
2. Аксиомы теории вероятностей вводятся так, чтобы вероятность события обладала основными свойствами частоты.
3. Отправляясь от основных свойств вероятности, присущих частотному и классическому определениям, аксиоматическое определение вероятности охватывает эти определения как частные случаи.
4. Формальное построение теории вероятностей показывает, что язык этой теории есть язык теории множеств, а точнее, теории меры. Однако прикладные задачи формулируются на языке практики. Поэтому в некоторых сомнительных случаях приходится полностью описывать вероятностную задачу с указанием тройки вероятностного пространства.
Основоположник современного абстрактного построения теории вероятностей А.Н. Колмогоров неоднократно указывал на необходимость очень вдумчивого согласования абстрактной теории с прикладными вопросами. Его ученик Б.В. Гнеденко отмечает, что абстрактное изложение предмета имеет ряд преимуществ. Однако, специалистам-прикладникам трудно знакомиться с наукой по абстрактным книгам, ибо "такие книги не создадут так необходимого мостика между потребностями практики и математической теорией" [4]. Поэтому в настоящем учебнике делается попытка создать такой мостик с помощью большого количества примеров, а, с другой стороны, изложением основ аксиоматического подхода в построении теории вероятностей.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 4741; Нарушение авторских прав?; Мы поможем в написании вашей работы!