
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема сложения вероятностей
|
|
|
|
Теорема сложения вероятностей позволяет вычислять вероятности суммы двух или нескольких событий. Для двух событий теорема формулируется следующим образом.
Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения:
P(A+B)= P(A) + P(B) – P(AB). (1.13.1)
Докажем теорему для схемы случаев. Пусть общее число элементарных исходов равно N, причем k из них влекут за собой событие А, l исходов - событие В и m - событие АВ (рис. 1.14). Из условия и рис.1.14 следует, что вероятности событии А, В и АВ равны: P(A)= k/N, P(B)= l/N, P(AB)= m/N.
Объединению (сумме) событий А и В благоприятствует k+(l-m) событий. Следовательно,
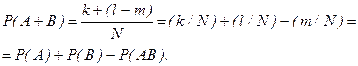
Теорему сложения вероятностей можно обобщить на случай, когда число событий больше двух. Так, например, формула для вычисления вероятности суммы трех совместных событий имеет вид
P(A+B+C)= P(A)+P(B)+
+P(C)-P(AB)-P(AC)-P(BC)+P(ABC). (1.13.2)
 Теорема сложения доказывается только для схемы случаев. Если ситуация к схеме случаев не сводится, то теорема обосновывается тем, что приведенные в доказательстве соотношения справедливы для относительных частот. Действительно, если при Nc испытаниях событие А появилось kc раз, событие В - lc раз и событие АB - mc раз, то событие А+В осуществилось (kc+lc-mc) раз. Таким образом,
Теорема сложения доказывается только для схемы случаев. Если ситуация к схеме случаев не сводится, то теорема обосновывается тем, что приведенные в доказательстве соотношения справедливы для относительных частот. Действительно, если при Nc испытаниях событие А появилось kc раз, событие В - lc раз и событие АB - mc раз, то событие А+В осуществилось (kc+lc-mc) раз. Таким образом,
P*(A+B)= (kc+lc-mc)/Nc=(kc/Nc)+(lc/Nc)-(mc/Nc)=
= P*(A)+P*(B)-P*(AB). (1.13.3)
Если число Nc испытаний достаточно велико, то соотношения для частот переходят в соотношения для вероятностей, а формула (3) переходит в (1).
Из теоремы сложения вытекает ряд следствий.
Следствие 1. Вероятность суммы несовместных событий А1 и А2 равна сумме вероятностей этих событий:
P(А1+А2)= P(А1)+P(А2). (1.13.4)
В самом деле, если А1 и А2 несовместны, то Р(А1А2)=0. Тогда из (1) следует (4).
Следствие 2. Сумма вероятностей несовместных событий, составляющих полную группу, равна единице:
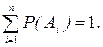 (1.13.5)
(1.13.5)
Действительно, пусть события А1, А2,..., Аn несовместны и составляют полную группу. Тогда по теореме сложения будем иметь
P(А1+А2+…+Аn)=P(А1)+P(А2)+…P(Аn).
Так как событие А1+А2+…+Аn достоверно, ибо оно осуществляется при каждом опыте и вероятность его равна единице, то
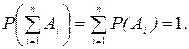
Следствие 3. Сумма вероятностей противоположных событий А и 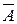 равна единице:
равна единице:
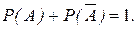 (1.13.6)
(1.13.6)
 |
Для доказательства учтем, что А и
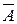 - несовместные события, образующие полную группу. Поэтому следствие 3 является частным случаем следствия 2. Оно выделено в виду его особой важности. Часто оказывается легче вычислить вероятность противоположного события
- несовместные события, образующие полную группу. Поэтому следствие 3 является частным случаем следствия 2. Оно выделено в виду его особой важности. Часто оказывается легче вычислить вероятность противоположного события 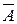 , чем прямого. Тогда сначала определяют Р (
, чем прямого. Тогда сначала определяют Р (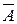 ), а затем находят вероятность Р(А) по формуле
), а затем находят вероятность Р(А) по формуле
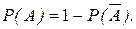 (1.13.7)
(1.13.7)
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1021; Нарушение авторских прав?; Мы поможем в написании вашей работы!