Оценка для дисперсии СВ

В качестве оценки для дисперсии рассмотрим следующую величину:

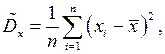(5)

(5) – выборочная дисперсия. Проверим ее на состоятельность и несмещенность. Преобразуем выражение (5) к другому виду:

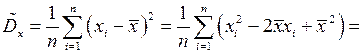
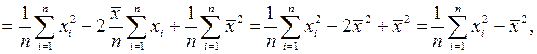
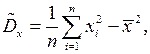(6)

в (6) первый член представляет собой среднее арифметическое наблюдаемых значений случайной величины 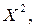значит он сходится по вероятности к 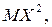второй член сходится по вероятности к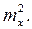

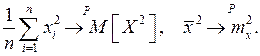
Следовательно, правая часть (6) сходится по вероятности к величине 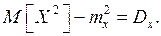Это означает, что (6) является состоятельной оценкой.

Теперь проверим, является ли выборочная дисперсия несмещенной оценкой:

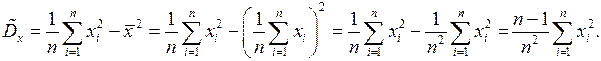
Так как дисперсия 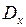не зависит от того, в какой точке выбрать начало координат, выберем его в точке 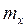затем найдем математическое ожидание величины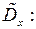

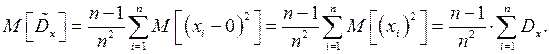
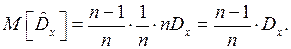(7)

Очевидно, выборочная дисперсия является смещенной оценкой. Однако, если умножить 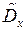на 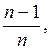то мы получим для 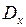оценку, обладающую свойством несмещенности, ибо:

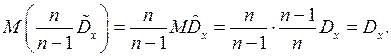
Эту оценку принято называть «исправленной» выборочной дисперсией и определять формулой:

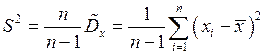(8)

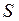- «исправленное» среднее квадратическое отклонение. Так как 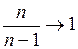при 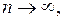то (8) будет также и состоятельной оценкой.

Дата добавления: 2014-01-03