Проверка гипотезы о значимости выборочного коэффициента корреляции

Пусть двумерная генеральная совокупность распределена по нормальному закону. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции . Выборочный коэффициент является оценкой для коэффициента корреляции и, в общем случае, отличается от него; более того, между величинами и 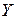может отсутствовать корреляционная зависимость. Следовательно, в силу того, что выборка случайна, из того, что выборочный коэффициент корреляции нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость при заданном уровне значимости 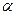проверить нулевую гипотезу при конкурирующей гипотезе 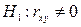. Если нулевая гипотеза 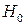отвергается, то это будет означать, что выборочный коэффициент корреляции является значимым (выборочный коэффициент корреляции значимо отличается от нуля), а случайные величины X и Y коррелированны, т.е. связаны корреляционной зависимостью. Если нулевая гипотеза 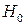будет принята, то это будет означать, что выборочный коэффициент корреляции не является значимым, а случайные величины X и Y некоррелированны. В качестве критерия возьмем случайную величину:

(24)

Известно (в случае нормального распределения (X,Y)), что эта случайная величина распределена по закону Стьюдента с степенями свободы. В силу того, что распределение Стьюдента является симметричным, критическую область удобно брать симметричной: _кр. Критическая точка _кр находится по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы . Затем вычисляют (по данным выборки) 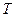_наб.

Если _набкр – нулевую гипотезу отвергают. Если _набкр, нет оснований отвергать нулевую гипотезу.

Пример 3. По выборке объемом n=8 из двумерной генеральной совокупности (X,Y), распределенной по нормальному закону, найден выборочный коэффициент корреляции =0,945. При уровне значимости 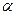=0,05 проверить нулевую гипотезу при альтернативной гипотезе .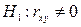

Решение: По уровню значимости и числу степеней свободы распределения Стьюдента находим критических точек распределения Стьюдента (для двусторонней критической области): 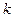_кр=2,45. Вычисляем наблюдаемое значение критерия по формуле (24): 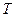_наб; _наб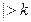кр, следовательно, нулевая гипотеза отвергается; случайные величины X и Y коррелированны.

Пример 4. По выборке объемом n=150 из двумерной генеральной совокупности (X,Y), распределенной по нормальному закону, найден выборочный коэффициент корреляции =0,7. При уровне значимости проверить нулевую гипотезу при альтернативной гипотезе .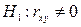

Решение: Вычислим сначала наблюдаемое значение критерия: 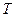_наб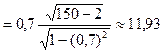. Критическая точка _кр может быть найдена по таблице распределения Стьюдента (для двусторонней критической области) по и числу степеней свободы =148; имеем _кр=2,58. _набкр. Отсюда делаем вывод: нулевая гипотеза отвергается. Следовательно, выборочный коэффициент корреляции является значимым; между X и Y существует корреляционная связь.

Дата добавления: 2014-01-03