Формула Байеса (теорема гипотез)

Формула Байеса является решением следующей задачи. Пусть событие А может произойти только при появлении одного из несовместных событий (гипотез) H₁, H₂,... H_n. Предполагается, что известны априорные вероятности гипотез Р(H₁), Р(H₂),..., Р(H_n) и условные вероятности перехода Р(А/H_i), i= 1,2,…,n, события А при каждой из гипотез (рис. 1.20). Допустим, что произведено испытание, в резуль­тате которого появилось событие А. Необходимо определить, с какой из гипотез следует связывать появление события А, т.е. определить, следствием какой гипотезы явилось это событие. Иначе говоря, требуется определить обратные вероятности гипотез Р(H₁/A), Р(H₂/A),…, Р(H_n/A) при условии, что событие A произошло. Если событие А произошло, то это, очевидно, должно вызвать переоценку вероятностей гипотез H_i, i= 1,2,…,n. Количественную оценку изменения вероятностей гипотез дает формула Байеса.

Вероятность гипотезы Р(H_i/A) равна отношению вероятности Р(H_iA) совместного появления событий H_i и А к полной вероятности Р(А) события А:

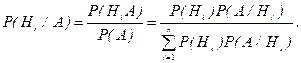(1.16.1)

Вывод формулы Байеса основан на использовании теоремы умножения вероятностей. В данном случае события H_i и А совместны и зависимы. Поэтому

P(AH_i)= P(A)P(H_i/A)= P(H_i)P(A/ H_i).

Следовательно,

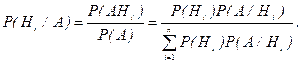
Поясним смысл составляющих, входящих в эту формулу.

Первая часть выражения (1) состоит из двух сомножителей: априорной вероятности P(H_i), характеризующей неопределенность гипотезы H_i до опыта и коэффициента 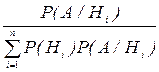, уточняющего априорную вероятность на основе эксперимента. Апостериорная вероятность P(H_i/А) гипотезы H_i характеризует пересмотренное значение априорной вероятности P(H_i) после получения дополнительной информации о появлении события А. Вероятность P(А/H_i) события А (наблюдения, сообщения и т.п.) в предположении, что верна гипотеза H_i иногда называют правдоподобием гипотезы H_i.

Формула Байеса (1) позволяет определить вероятности гипотез после того, как появилось событие А. Необходимость в проведении эксперимента возникает тогда, когда априорные вероятности кажутся недостаточно надежными и требуют уточнения. Из формулы видно, что при определении апостериорной (обратной) вероятности P(H_i/А) нужно учитывать как первоначальные (априорные) данные о гипотезах, характеризуемых вероятностью P(H_i), так и результаты опыта (произошло событие А, а не какое-либо другое), т.е. апостериорные (после опытные) сведения.

Формула Байеса играет фундаментальную роль в современной статистике и теории оптимального радиоприема. С её помощью можно, получив некоторое сообщение (сигнал), вычислить обратные вероятности всех сообщений, которые в действительности могли быть переданы и за истинное принять значение, обратная вероятность P(H_i/А) которого максимальна. При этом решении не исключены ошибки. Однако они будут минимальными по сравнению с другими решениями. Чтобы иметь надежные результаты для принятия решения иногда проводятся последовательные эксперименты. В таком случае апостериорные вероятности гипотез после первого эксперимента принимаются в качестве априорных вероятностей для второго эксперимента и т.д.

Методика решения задач с применением формулы Байеса такова. Во-первых, необходимо вычислить вероятности гипотез при условии, что произошло событие А, т.е. вычислить апостериорные вероятности P(H_i/А), i= 1,2,…,n. Во-вторых, сравнить полученные вероятности между собой. В-третьих, принять решение, т.е. отдать предпочтение той гипотезе, которая имеет наибольшую вероятность.

Дата добавления: 2014-01-03