
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема о повторении опытов (формула Я. Бернулли)
|
|
|
|
В теории вероятностей встречаются задачи, в которых один и тот же опыт (испытание) повторяется многократно. В подобных случаях требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Рассмотрим один из примеров. На вход приёмника поступает серия импульсов, отражённых от радиолокационной цели, амплитуды которых приблизительно одинаковы. Появление каждого импульса можно рассматривать как опыт, в результате которого импульс может либо пройти (успех) на выход приёмника (событие А), либо не пройти (неудача) из-за подавления помехами (событие 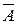 ). Требуется найти вероятность того, что на выход приёмника пройдет определённое число импульсов (0, 1, …, n). Подобные задачи решаются с помощью теоремы о повторении опытов, которая утверждает следующее.
). Требуется найти вероятность того, что на выход приёмника пройдет определённое число импульсов (0, 1, …, n). Подобные задачи решаются с помощью теоремы о повторении опытов, которая утверждает следующее.
Если производится n независимых опытов, в каждом из которых вероятность появления события А постоянна и равна p, а вероятность противоположного события 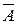 есть q= 1- p, то вероятность Pn(k) того, что при этих опытах событие A появится ровно k раз, где k = 0, 1, 2,..., п, равна
есть q= 1- p, то вероятность Pn(k) того, что при этих опытах событие A появится ровно k раз, где k = 0, 1, 2,..., п, равна
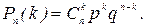 (1.17.1)
(1.17.1)
Докажем это утверждение. Интересующее нас событие (при n независимых опытах событие А появится ровно k раз) распадается на несколько частных случаев:
событие А появилось в первых k опытах и не появилось при (n-k) последующих: 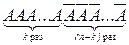 . Вероятность такого варианта по теореме умножения для независимых событий равна P(A)P(A)…P(A)P(
. Вероятность такого варианта по теореме умножения для независимых событий равна P(A)P(A)…P(A)P( 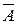 )P(
)P( 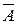 )…P(
)…P( 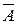 )= pk( 1 -p)n-k= pkqn-k.
)= pk( 1 -p)n-k= pkqn-k.
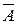 )P(A)P(A)…P(A)P(
)P(A)P(A)…P(A)P( 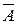 )P(
)P( 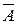 )…P(
)…P( 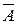 )= pk( 1 -p)n-k= pkqn-k.
)= pk( 1 -p)n-k= pkqn-k.
Всего таких вариантов будет столько, сколько можно составить сочетаний из n элементов по k. Так как варианты между собой несовместны, то по теореме сложения вероятностей несовместных событий получим
Рn(k)= pkqn-k+pkqn-k+…+ pkqn-k=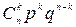 .
.
Таким образом, вероятность Рn(k) того, что при n повторениях опыта событие A появится ровно k раз равна
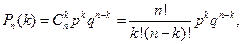
где q= 1 -p, k= 0, 1,…, n.
С помощью формулы Бернулли можно решать также следующие задачи.
1. Вычислить вероятность того, что при n независимых опытах событие А появится не менее m раз, т.е. k= m, m+ 1,…, n:
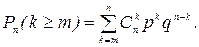 (1.17.2)
(1.17.2)
2. Определить вероятность того, что при n опытах событие A появится не более m раз, т.е. когда k= 0, 1,…, m:
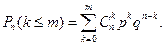 (1.17.3)
(1.17.3)
3. Найти вероятность того, что при n опытах событие А появится от m1 до m2 раз, т.е. когда k= m1,…, m2:
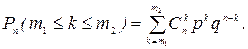 (1.17.4)
(1.17.4)
4. Определить вероятность того, что при n опытах событие A появится хотя бы один раз, т.е. когда k= 1, 2,…, n:
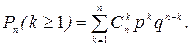 (1.17.5)
(1.17.5)
Формула Бернулли часто используется в качество математической модели реальных ситуаций: при кодировании сообщений, контроле качества продукции, определении надежности систем и т.д. Рассмотренная схема называется схемой независимых испытаний или схемой Бернулли. Она определяется заданием натурального числа n и произвольного р (0£ р £1). Важность формулы Бернулли определяется тем, что она связана с повторением испытаний в одинаковых условиях, т.е. с такими условиями, в которых как раз и проявляются законы теории вероятностей.
Известно несколько обобщении формулы Бернулли [2,5]. Одно из них относится к случаю, когда из-за меняющихся условий при проведении n независимых опытов вероятность р меняется от опыта к опыту. Второе обобщение имеет в виду, что каждый опыт может иметь не два, а большее число исходов.
Особо важное значение для практики имеет обобщение схемы независимых испытаний, приводящее к схеме цепей Маркова (см. §7.2).
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 3073; Нарушение авторских прав?; Мы поможем в написании вашей работы!