Корреляционный анализ

Корреляционно-регрессионный анализ включает измерение тесноты и направления связи (корреляционный анализ), а также установления аналитического выражения формы связи (регрессионный анализ).

В статистике принято различать следующие виды корреляции:

- Парная корреляция – связь между двумя признаками (результативным и факторным);

- Множественная корреляция – связь между результативным и двумя или более факторными признаками;

- Частная корреляция – связь между результативным и одним из факторных признаков при фиксированном значении других признаков.

Количественно оценить тесноту и направление связи между двумя признаками при парной корреляции можно с помощью линейного коэффициента корреляции.

Линейный коэффициент корреляции - характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. Этот коэффициент применяется при исследовании социально-экономических явлений, распределение которых близко к нормальному.

r =r =

Линейный коэффициент корреляции может принимать значения от -1 до 1.

При r = 0 связь отсутствует.

Если 0 < r < 1 – связь прямая; с увеличением x увеличивается y.

Если -1 < r < 0 – связь обратная; с увеличением x уменьшается y, и наоборот.

При r = 1 - связь функциональная; каждому значению факторного признака строго соответствует одно значение результативного признака.

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза [r=0]

Если расчетное значение больше табличного ()

,

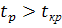то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции (r) и, следовательно, и о статистической существенности зависимости между x и y.

Данный критерий оценки значимости () применяется для совокупности с числом наблюдений менее 50 (n<50).

При n>100: .

В случае, если заранее известно, что связь нелинейная, то рассчитывается корреляционное отношение и индекс корреляции.

Корреляционное отношение характеризует силу связи при любой форме связи.

ŋ=ŋ=

- теоретическое значение признака

y – индивидуальное значение результативного фактического признака

Факторная дисперсия:

Общая дисперсия результативного признака:

Корреляционное отношение не показывает направление связи. Значение меняется [0;1], чем ближе к 1, тем теснее связь.

Индекс корреляции: R=

Индекс корреляции рассчитывается для всех форм связи, направления не показывает, учитывает лишь величину.

Дата добавления: 2014-01-03