Непараметрические методы оценки корреляционной связи

При использовании непараметрической оценки связи показателям присваивается порядковый номер или ранг.

Коэффициенты, предложенные для изучения корреляционной связи на основе ранга:

1. Коэффициент Спирмена – используется, когда используются два признака.

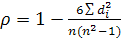[-1; 1]

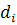- разница рангов;

n – число наблюдений (пар рангов).

Показатель может принимать значения от -1 до 1, чем ближе значение к 1, тем теснее связь.

2. Если присутствует несколько признаков для изучения, то для оценки связи используется коэффициент конкордации:

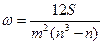
m – число факторов;

n – число ранжируемых единиц;

S – сумма квадратов отклонений рангов.

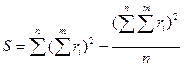
r – ранг по показателям.

Показатель может принимать значения от -1 до 1, чем ближе значение к 1, тем теснее связь.

3. Если каждый из признаков представлен в виде альтернативного значения, причем парного (да-нет), то теснота связи в этом случае определяется с помощью коэффициентов ассоциации и контингенции.

Для расчета данных коэффициентов используются таблицы «четырех полей», частоты которых обозначаются через a, b, c, d.

a	b	a + b
с	d	c + d
a + c	b + d	a + b + c + d

Коэффициент ассоциации рассчитывается по следующей формуле:

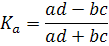
Если хотя бы один из четырех показателей таблицы «четырех полей» отсутствует, то коэффициент ассоциации равен 1, что дает преувеличенную оценку тесноты связи между признаками. В данном случае можно использовать коэффициент контингенции:

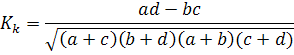
Коэффициент контингенции 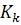всегда меньше коэффициента ассоциации .

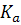Связь считается подтвержденной, если 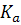≥0,5, а 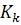≥0,3.

4. Если качественные признаки представлены большим числом показателей (более 2), то рассчитывается коэффициент взаимной сопряженности (коэффициент Пирсона).

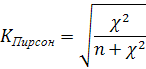
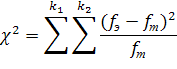
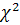- показатель взаимной сопряженности

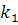- число значений или групп первого признака

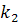– число значений второго признака

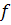- отношение произведений итоговых частот соответствующих строки и столбца к итоговой частоте (общему итогу).

Дата добавления: 2014-01-03