Регрессионный анализ

Регрессионный анализ заключается в определении аналитического выражения связи, в которой изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения.

Регрессия может быть однофакторной (парной) и многофакторной (множественной).

По форме зависимости различают линейную и нелинейная регрессию.

Парная регрессия характеризует связь между двумя признаками факторным и результативным. Аналитическая связь между ними описывается:

- прямой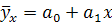

- гиперболы

- параболы .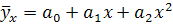

Определить тип управления можно следующим образом:

- если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то связь между ними – линейная;

- если результативный и факторный признаки изменяются в обратной пропорции, то связь – гиперболическая;

- если факторный признак увеличивается в арифметической прогрессии, а результативный – значительно быстрее, то используется параболическая или степенная регрессия.

Оценка параметров уравнения регрессии (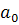,,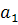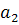) проводится на основании метода наименьших квадратов МНК.

Если результативный признак с увеличением факторного равномерно возрастает или убывает, то связь линейная, выражается уравнением прямой

.

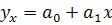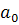– коэффициент, который учитывает влияние прочих (неучтенных) факторов;

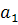– коэффициент регрессии, характеризующий изменение результативного признака при изменении факторного на единицу собственного измерения. 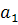- основной коэффициент в уравнении и учитывает основное влияние.

МНК:

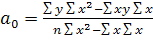
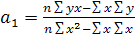
Если исследуемые признаки имеют разные единицы измерения, то для оценки влияния используется коэффициент эластичности:

Он характеризует изменение результативного признака при изменении факторного признака на 1%.

Если значения факторного признака расположены в порядке геометрической прогрессии и определенному значению результативного признака соответствует факторный, также в геометрической прогрессии, то связь можно выразить степенной функцией:

.

Данную функцию приводят к линейному виду путем логарифмирования:

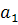– коэффициент эластичности.

Если результативный признак с увеличением факторного признака возрастает не бесконечно, а стремится к конечному пределу, то исследуемые показатели описываются гиперболой:

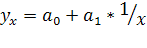
Оценка адекватности моделей, построенных на основании уравнений регрессии, начинается с проверки значимости коэффициентов регрессии с помощью t-критерия Стьюдента:

- дисперсия коэффициента регрессии

Параметр модели признается значимым, если выполняется условие:

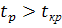(α, n=n-k-1)

α – уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь.

n=n-k-1 – число степеней свободы или число свободно варьирующих элементов совокупности

Дисперсию можно определить по зависимости:

=,

где - дисперсия результативного признака;

k - число факторных признаков в уравнении.

Проверка адекватности регрессионной модели в целом осуществляется с помощью F-критерия Фишера и величины средней ошибки аппроксимации ().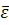

Расчетное значение F-критерия Фишера определяется по зависимости:

Если при α=0,01 или α=0,05, то гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим отвергается.

Величина 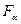определяется по специальным таблицам, входом в которые являются величины α=0,01 или α=0,05и числа степеней свободы: v₁=k-1, v₂=n-k, где n – число наблюдений, k – число факторных признаков в уравнении.

Значение средней ошибки аппроксимации определяется по следующей зависимости:

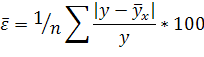
Значение не должно быть больше 12-15%.

Дата добавления: 2014-01-03