Критерій узагальненого максиміну (песимізму - оптимізму) Гурвіца

Прийняття рішень в умовах невизначеності

При прийнятті рішень в умовах невизначеності, коли імовірності можливих варіантів обставин невідомі, можуть бути використані ряд критеріїв, вибір кожного з яких, нарівні з характером задачі, що вирішується, поставлених цільових установок і обмежень, залежить також від схильності до ризику осіб, що приймають рішення.

До числа класичних критеріїв, які використовуються при прийнятті рішень в умовах невизначеності, можна віднести:

- принцип недостатнього обгрунтування Лапласа;

- максимінний критерій Вальда;

- мінімаксний критерій Севіджа;

Принцип недостатнього обгрунтування Лапласа використовується у разі, якщо можна припустити, що будь-який з варіантів обставин не більш вірогідний ніж інший. Тоді імовірності обставин можна вважати рівними і проводити вибір рішення так само, як і в умовах ризику - по мінімуму середньовиваженого показника ризику, тобто, перевагу потрібно надати варіанту, який забезпечує мінімум у виразі:

_{n n}

R _i = å H _{i j} P_j = å H _ij 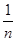i = 1, m

^{j=1 j=1}

де n - кількість варіантів обставин, що розглядаються.

Розглянемо вибір варіантів в умовах невизначеності з використанням принципу недостатнього обгрунтування Лапласа за початковими даними наведеними в розділі 6.1 прикладу.

При обліку трьох варіантів обставин (n = 3) імовірність кожного варіанту складає 0,33.

Тоді, з врахуванням приведених даних про втрати для кожної пари комбінацій рішень Р і обставин О (табл. 6.3) і імовірності кожного варіанту обставин рівної 0,33, середньовиважений показник ризику для кожного з рішень буде складати:

R₁ = 0,55 × 0,33 + 0,47 0,33 + 0,00 × 0,33 = 0,3366;

R₂ = 0,05 × 0,33 + 0,62 × 0,33 + 0,10 × 0,33 = 0,2541;

R₃ = 0,45 × 0,33 + 0,00 × 0,33 + 0,3 × 0,33 = 0,2475;

R₄ = 0,00 × 0,33 + 0,72 × 0,33 + 0,05 × 0,33 = 0,2541.

Як оптимальне потрібно вибрати варіант рішення Р₃.

Як бачимо, в початковому прикладі (розділ 6.1) найкращим, з точки зору прийнятого критерію (середньовиваженого показника ризику), було рішення Р₄.

Таким чином, зміна імовірності настання варіантів обставин призвела до зміни варіанту рішення, якому потрібно надати перевагу.

Максимінний критерій Вальда використовується у випадках, коли потрібна гарантія, щоб виграш в будь-яких умовах виявлявся не менш, ніж найбільший з можливих у гірших умовах..

Найкращим рішенням буде таке, для якого виграш виявиться максимальним з усіх мінімальних при різних варіантах умов.

Критерій, що використовується при такому підході, отримав назву максиміна. Його формалізований вираз

max min a_ij

^{i j}

Як бачимо, вихідними даними при виборі варіантів рішень за критерієм Вальда є виграші а _ij, відповідні кожній парі комбінацій рішень Р і обставин О.

Скористаємося наведеним раніше прикладом (зокрема, матрицею ефективності рішень, наведеною в табл. 6.2) для ілюстрації вибору оптимального варіанту по критерію Вальда.

Мінімальна віддача по варіантах виділена "жирним" шрифтом в табл. 6.4.

Таблиця 6.4. Ефективність випуску нових видів продукції

Варіанти	Варіанти обставин
рішень	О1	О2	О3
Р1	0,25	0,35	0,40
Р2	0,75	0,20	0,30
Р3	0,35	0,82	0,10
Р4	0,80	0,20	0,35

З табл. 6.4 випливає, що максимальний з мінімальних результатів дорівнює 0,25 і, отже, перевагу необхідно надати варіанту Р₁, що забезпечує цей результат. Це максимальний гарантований результат (виграш), який може бути отриманий в умовах початкових даних, що є. Вибравши рішення Р₁, ми незалежно від варіантів обставини отримаємо виграш не менше за 0,25. При будь-якому іншому рішенні, у випадку несприятливої обставин може бути отриманий результат (виграш) менше 0,25.

Так, при виборі рішення Р₂ отриманий виграш, в залежності від варіанту обставин, що наступив, буде коливатися від 0,2 до 0,75. Для рішень Р₃ і Р₄ межі, в яких буде коливатися виграш, складуть відповідно 0,10… 0,82 і 0,20 … 0,80.

Даний критерій простий і чіткий, але консервативний в тому значенні, що орієнтує того, що приймає рішення на дуже обережну лінію поведінки. Так, цей критерій ніяк не враховує, що, в разі прийняття рішення Р₁ (тобто при орієнтації на виграш 0,25), максимальний виграш не перевищує 0,4. У той час як, вибираючи, наприклад, рішення Р₄, при гарантованому виграші 0,20, в разі сприятливої обставини можна отримати виграш, що дорівнює 0,80.

Тому критерієм Вальда, головним чином, користуються у випадках, коли необхідно забезпечити успіх при будь-яких можливих умовах.

Мінімаксний критерій Севіджа використовується в тих випадках, коли потрібно в будь-яких умовах уникнути великого ризику.

Відповідно до цього критерію перевагу потрібно надати рішенню, для якого втрати, максимальні при різних варіантах умов, виявляться мінімальними. Його формалізований вираз

min max Н_ij

^{i j}

де Н_ij - втрати, відповідні і-му рішенню при j-му варіанті обставин.

Цей критерій також відноситься до розряду обережних. Однак, на відміну від критерію Вальда, який направлений на отримання гарантованого виграшу, критерій Севіджа мінімізує можливі втрати.

Тут, як початкові дані при виборі рішень, виступають втрати (Н_ij), відповідні кожній парі комбінацій рішень Р і обставин О.

Для ілюстрації вибору за критерієм Севіджа скористаємося наведеним вище прикладом (зокрема, матрицею втрат, наведеною в табл. 6.3).

Максимальні втрати за варіантами виділені "жирним" шрифтом в табл. 6.5.

Таблиця 6.5 Величина втрат при випуску нових видів продукції

Варіанти	Варіанти обставин
рішень	О1	О2	О3
Р 1	0,55	0,47	0,00
Р 2	0,05	0,62	0,10
Р 3	0,45	0,00	0,30
Р 4	0,00	0,72	0,05

З табл. 6.5 випливає, що мінімальні з максимальних втрати складають 0,45 і, отже, перевагу необхідно надати варіанту Р₃, що забезпечує ці втрати.

Вибір варіанту рішення Р₃ гарантує, що у разі несприятливої обставини, втрати не перевищать 0,45. У той час як для рішень Р₁, Р₂ і Р₄, у випадку несприятливої обставини, втрати складуть відповідно: 0,55; 0,62 і 0,72.

Основним початковим допущенням цього критерію є припущення про те, що на настання варіантів обставин впливають дії розумних противників (конкурентів), інтереси яких прямо протилежні інтересам особи, що приймає рішення. Тому, якщо у противників (конкурентів) є можливість витягнути які-небудь переваги, то вони це обов'язково зроблять. Ця обставина примушує особу, що приймає рішення забезпечити мінімізацію втрат внаслідок цих дій.

Критерій узагальненого максиміну (песимізму - оптимізму) Гурвіца використовується, якщо потрібно зупинитися між лінією поведінки з розрахунку на гірше і лінією поведінки з розрахунку на краще.

У цьому випадку перевага віддається варіанту рішень, для якого виявиться максимальним показник G, що визначається з виразу:

Gi = {k × min a_ij + (1-k) max a_ij },

^{j j}

де k - коефіцієнт, що розглядається як показник оптимізму (0 £ k £ 1), при k = 0- лінія поведінки з розрахунку на краще, при k = 1 - з розрахунку на гірше;

a_ij - виграш, відповідний i- му рішенню при j-му варіанті обставин.

Неважко пересвідчитися, що при k = 1 критерій Гурвіца співпадає з критерієм Вальда, тобто орієнтація на обережну поведінку. При k = 0 - орієнтація на граничний ризик, так як великий виграш, як правило, пов'язаний з великим ризиком. Значення k між 0 і 1 є проміжними між ризиком та обережністю і вибираються в залежності від конкретної обставини та схильності до ризику особи, що приймає рішення.

У табл. 6.6 наведені значення показника G для різних варіантів рішень в залежності від величини коефіцієнта k.

Таблиця 6.6 Значення показника G для різних k

Рішення	Значення коефіцієнта k
	0,00	0,25	0,50	0,75	1,00
P1	0,400	0,362	0,325	0,287	0,250
Р2	0,750	0,612	0,475	0,337	0,200
Р3	0,820	0,640	0,460	0,280	0,100
Р4	0,800	0,650	0,500	0,350	0,200
Оптимальне рішення	Р3	Р4	Р4	Р4	P1

Як бачимо, зі зміною коефіцієнта k змінюється варіант рішення, якому потрібно надати перевагу.

Нами розглянуті найбільш загальні (класичні) методи, які дозволяють обгрунтовувати та приймати рішення при невизначеності економічних даних і ситуацій, нестачі фактичної інформації про навколишнє середовище і перспективних її змін.

Потрібно зазначити, що розроблені економічною теорією і практикою, способи і прийоми розв`язання задач в умовах ризику і невизначеності не обмежуються переліченими методами. У залежності від конкретної ситуації в процесі аналізу використовуються й інші методи, що сприяють розв`язанню задач, пов'язаних з мінімізацією ризику.

Деякі з них, зокрема, використання середньоквадратичного відхилення (s) і коефіцієнта варіації (V), як міри ризику, будуть розглянуті нижче.

Дата добавления: 2014-01-03