Урахування ризику при інвестуванні капітальних вкладень

T

.

100

. 96

1 2 3

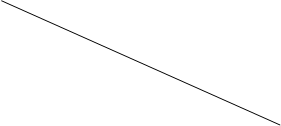
Рис. 6.1.

Як видно з рис. 6.1, при вказаних співвідношеннях `Х і s, перший варіант забезпечує більш високе мінімальне значення віддачі при всіх рівнях довірчої імовірності. Таким чином, в даному конкретному прикладі є однозначне рішення - перший варіант є переважним і виcновки, зроблені на основі існуючих підходів до оцінки варіантів [7,12,22,34], будуть помилковими.

Змінимо початкові дані наведеного вище прикладу. Нехай співвідношення між Х і s по варіантах буде наступним: `Х<sub>1</sub> = 110; s<sub>1 =</sub> 10; `Х _{2 =} 100; s = 5.

Неважко побачити, що і в цьому випадку при використанні коефіцієнта варіації перевагу потрібно віддати другому варіанту.

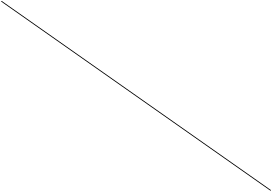
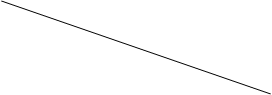
На рис. 6.2 показана залежність мінімальних значень віддачі по варіантах для різних значень t.

Як видно з рис. 6.2, при вказаних співвідношеннях ефективність варіантів залежить від рівня довірчої імовірності. При довірчій імовірності, що не перевищує 0,9545 (t = 2), кращим потрібно визнати перший варіант, в противному випадку перевагу потрібно віддати другому варіанту.

Зі зміною значень `Х і s по варіантах буде змінюватися і область їх ефективності.

Х

110

100

95 90

t

1 2 3

Рис.6.2

Як показав виконаний нами аналіз, ефективність варіантів залежить від співвідношення D`Х і D s, які характеризують відповідно додаткову віддачу і додаткову варіацію варіанту з більшою очікуваною віддачею.

Використовуючи точку, в якій мінімальна віддача по варіантах, що порівнюються рівна (`Х<sub>1</sub> - t s<sub>1</sub> = `Х₂ - t s₂), отримаємо аналітичне вираження, що відображає цю залежність:

`X<sub>1</sub> -`X ₂ D`X

= = t

s₁ - s₂ D s

При t ³ 3 однозначно кращим буде варіант, що забезпечує більшу очікувану віддачу.

При t < 3 вибір варіанту залежить від необхідної довірчої імовірності.

У загальному випадку, якщо особі, що приймає рішення, відома (або прийнята) необхідна довірча імовірність (і, як наслідок, відповідне їй значення t), то перевагу потрібно віддати варіанту, який забезпечує максимум у виразі

`Х _i - t s _i = max

Аналіз вираження `Х _i - t s _i дозволяє також розглянути спектр можливих результатів рішень при різних рівнях прийнятої довірчої імовірності.

Однією з початкових передумов представлених вище міркувань, було допущення про нормальний розподіл випадкової величини.

Разом з тим, неважко довести, що отримані результати і висновки об`єктивні незалежно від закону розподілу випадкової величини.

Так, відповідно до відомої нерівності Чебишева, імовірність того, що відхилення випадкової величини по модулю від своєї середньої більше заданого числа D, не перевищує її дисперсії розділеної на квадрат цього числа, тобто

P{½x -`x½ ³ D } £ s² / D²

Задаючи певну граничну імовірність, можна визначити відповідну їй величину відхилення D_p

D_p £ Ö s²/P

На основі нерівності Чебишева можна затверджувати, що імовірність того, що відхилення випадкової величини по модулю від свого математичного очікування не перевищує певної заданої величини, визначиться з виразу

P{½x-`x ½ < D} > 1 - (s² / D²)

Отже, з імовірністю не менше за 1- р можна затверджувати, що

Х_min ³ `X - D_p

Скористаємося приведеними раніше прикладами і визначимо граничні значення віддачі (Х_min) по варіантах для різних рівнів довірчої імовірності. Для цього приймемо значення D рівним відповідно 2s, 3s і 4s.

Неважко побачити, що при: D _p = 2s, Р £ 0,250; D _p= 3s, Р £ 0,111; D _p = 4s, Р £ 0,062.

Розглянемо перший приклад порівняння варіантів, коли `Х<sub>1</sub> = 110, s<sub>1</sub> = 7, а `Х₂ = 100, s₂ = 5.

З імовірністю не менше за 0,75 можна затверджувати, що мінімальне значення віддачі по варіантах складе відповідно 96 і 90 одиниць, з імовірністю не нижче за 0,938 - мінімальні значення віддачі по варіантах складуть відповідно 82 і 80 одиниць.

Як бачимо і при такому підході перевага віддана другому варіанту по величині коефіцієнта варіації або на основі того, що менша дисперсія характеризує менший ризик, є помилковим.

Неважко побачити, що для другого прикладу, коли `Х₁ = 110, s_{1 =}10, а Х₂ = 100, s_{2 =} 5, як і при використанні нормального закону розподілу, ефективність варіантів буде залежати від необхідної довірчої імовірності.

Як бачимо, відмінність в підході полягає тільки в тому, що використання нормального закону дозволяє більш суворо і однозначно відкинути розглянуті вище існуючі підходи до порівняльної оцінки варіантів по ступеню ризику.

У випадку, якщо закон розподілу відрізнений від нормального або невідомий, можна запропонувати наступний критерій порівняльної оцінки - перевагу потрібно віддати варіанту, що забезпечує максимум у виразі

`Xi - D _{р =} max

В умовах ринкової економіки, особливо в період її становлення, інвестування розвитку зв'язане з ризиком неотримання очікуваних результатів у встановлені (бажані) терміни.

У зв'язку з цим виникає необхідність кількісної оцінки міри ризику коштів, що інвестуються, з тим, щоб зазделегідь, ще до здійснення капітальних вкладень, потенційні інвестори, включаючи і саме підприємство, що планує будівництво, могли мати ясну картину реальних перспектив отримання прибутку і повернення вкладених коштів.

У цих умовах методичні підходи до оцінки економічної доцільності інвестиційних проектів повинні передбачати забезпечення мінімально гарантованого рівня прибутковості проекту при умові компенсації інфляційної зміни купівельної здатності грошей протягом періоду часу, що розглядається і покриття ризику інвестора, пов'язаного із здійсненням проекту. Це досягається шляхом використання методів дисконтування.

Дата добавления: 2014-01-03