Пример. Рассмотрим модель падения тела под углом к горизонту

Рассмотрим модель падения тела под углом к горизонту. Она дает возможность получить информацию о координатах траектории, заданных в осях (x, y):

y = – x ² + 4 x – 3.

Данная модель связывает две переменные y и x законом f (y, x) = 0. Координаты тела в полете изображены на рис. 1.8.

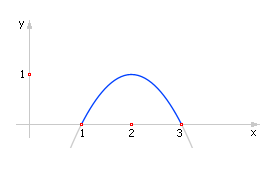
Рис. 1.8. Траектория движения тела,
брошенного под углом к горизонту

Модель может быть расширена введением некоторых исходных данных, например, нас, интересуют не все возможные значения y, а только точки на поверхности Земли. В этом случае модель примет вид:

y = – x ² + 4 x – 3, y = 0.

Такие уравнения могут появляться и исчезать в зависимости от исследуемой проблемы. Обычно их называют гипотезами.

Теперь поставим вопрос: «При каких значениях x тело окажется на поверхности Земли?»

В такой постановке модель и вопрос вместе образовали задачу:

y = – x ² + 4 x – 3,
y = 0,
x =?

Модель подразумевает, что исследователь может решать с её помощью прямые и обратные задачи.

Прямая задача не требует алгебраических преобразований, достаточно только арифметических подстановок:

x = 2, y = – x ² + 4 x – 3, y =?.

Ответ: y = 1. То есть, если на вход модели подать значение 2, то на выходе модели будет значение 1 — см. рис. 1.9.

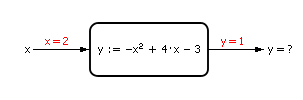
Рис. 1.9. Вид модели для решения прямой задачи

Обратная задача:

y = 0, y = – x ² + 4 x – 3, x =?

Ответ: x = 1, x = 3.

То есть ответ говорит: чтобы на выходе модели обеспечить значение 0, надо, чтобы на вход модели было подано значение 1 (или 3).

И в первом, и во втором случае мы в разной мере преобразовывали модель, но всегда так, чтобы на входе у неё была известная величина, а на выходе — неизвестная.

В первом варианте y = – x ² + 4 x – 3.

Во втором варианте модель преобразуется к виду: 0 = – x ² + 4 x – 3.

Решая обратную задачу мы опустили ряд преобразований, известных из курса средней школы, а именно:

D:= b ² – 4 ac, где a = –1, b = 4, c = –3,

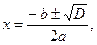
x:= 1 или x:= 3.

Преобразования происходили с учётом правил алгебры. Если бы правила алгебры были нам неизвестны, то решить обратную задачу нам бы не удалось. А значит, не удалось бы ответить на поставленный вопрос: «x =?».

Способность модели преобразовываться с помощью алгебры даёт возможность в дальнейшем использовать её многократно для решения различных задач, делать на ней прогнозы.

Поэтому, создавая модель, следует обязательно думать о том, какой алгеброй она будет преобразовываться. Создавать алгебру следует параллельно с моделью или использовать уже готовую алгебру и не отходить при построении модели от её правил.

Ещё один тип задач, который приходится решать на моделях — задачи настройки модели.

Пример. При каких значениях параметра a модель

y = ax ² + 4 x – 3

обеспечит y = 9 при x = 2?

Решаем систему уравнений:

y = a · x ² + 4 x – 3
y = 9
x = 2

получим ответ: a = 1.

От показанного на рис. 1.10 структурного изображения модели можно перейти к другому, математическому, её виду: Y = M (X).

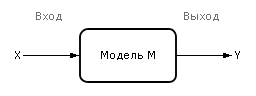
Рис. 1.10. Структурное изображение

Дата добавления: 2014-01-03