Проверка адекватности модели

Точек

При моделировании исследователя, прежде всего, интересует, насколько хорошо модель представляет моделируемую систему (объект моделирования). Одним из подходов в оценке адекватности состоит в сравнении выходов модели и реальной системы при одинаковых значениях входов. И те, и другие данные (данные, полученные на выходе модели и данные, полученные в результате эксперимента с реальной системой) – статистические. Поэтому для оценки адекватности применяют методы статистической теории оценивания и проверки гипотез.

Адекватность исследуемой модели можно проверить по дисперсиям отклонений откликов модели от среднего значения откликов системы.

Сравнение дисперсий проводят с помощью F- критерия (критерия Фишера)

,

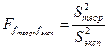где 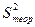− дисперсия, характеризующая ошибку модели;

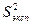− дисперсия, характеризующая ошибку эксперимента;

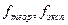- число степеней свободы модели и эксперимента соответственно.

Дисперсия, характеризующая ошибку модели, рассчитывается по формуле:

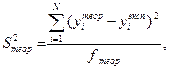
где 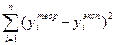- остаточная сумма квадратов, характеризующая

отклонение от регрессии;

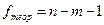- число степеней свободы модели;

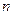− число экспериментальных точек;

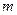− количество значимых коэффициентов модели в уравнении

регрессии, кроме коэффициента .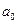

Числом степеней свободы в статистике называется разность между числом экспериментов и числом коэффициентов уравнения регрессии.

Для получения дисперсии, характеризующей ошибку эксперимента, проводят 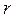параллельных экспериментов. По результатам этих экспериментов вычисляют дисперсию воспроизводимости эксперимента, характеризующую разброс значений отклика

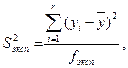
где 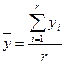- среднее арифметическое значение;

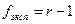- число степеней свободы параллельных экспериментов, равное количе­ству экспериментов минус единица. Здесь одна степень свободы исполь­зована для вычисления среднего.

Учитывая, что точность статистических оценок возрастает с ростом числа степеней свободы, число степеней свободы точной величины 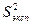можно принять равным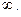

Значение 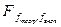сравнивается со значением, взятым из таблицы распределения Фишера в соответствии с уровнем значимости 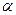и степенями свободы 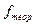и 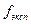. Если 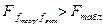− модель неадекватна (должна быть отвергнута, как недостаточно точная) и соответственно при 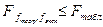− адекватна.

Таблица критерия Фишера построена следующим образом. Столбцы связаны с определенным числом степеней свободы для числителя 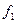, а строки – для знаменателя 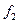. На пересечении соответствующих строки и столбца стоят критические значения F -критерия. Как правило, в технических задачах используется уровень значимости 0,05.

Проверка значимости коэффициентов. Значимость коэффициентов линейной регрессии определяется с помощью t – критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t – критерия

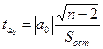- для параметра ;

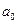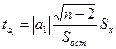- для параметра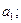

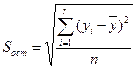- среднее квадратическое отклонение результативного признака от среднего арифметического значения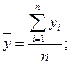

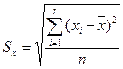- среднее квадратическое отклонение факторного признака от среднего арифметического значения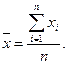

Вычисленные по вышеприведенным формулам значения сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости 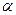и числом степеней свободы 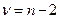. Если 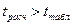, гипотеза о значимости коэффициента 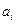принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.

Дата добавления: 2014-01-03