Линейная множественная модель

Включение в регрессионную модель новых переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности матричных обозначений. Матричное описание регрессии облегчает как теоретический анализ, так и необходимые расчетные процедуры.

Предположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно m (см. рис. 2.7):

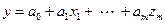. (2.8)

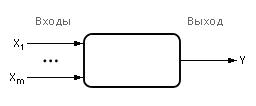
Рис. 2.7. Обозначение многомерного
черного ящика на схемах

Исходными данными при оценке параметров 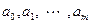является прямоугольная матрица входов Х и вектор результатов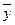

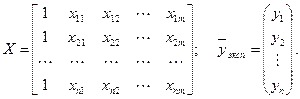(2.9)

Строки матрицы Х соответствуют результатам регистрации всех наблюдаемых параметров объекта в одном эксперименте, а столбцы содержат результаты наблюдений за одним параметром (фактором) во всех экспериментах. Первый столбец матрицы Х, состоящий из единиц, соответствует коэффициенту модели .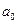

Уравнение регрессии (2.8) в матричной форме для данных (2.9) имеет вид

,

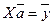где 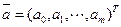- вектор-столбец параметров модели.

Применяя метод наименьших квадратов, нужно найти минимум суммы 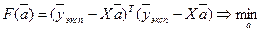. (2.10)

Учитывая, что при транспонировании произведения матриц получается произведение матриц, взятых в обратном порядке, т.е. 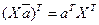после раскрытия скобок получим:

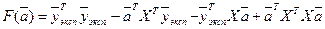. (2.11)

Произведение 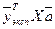есть матрица размера

,

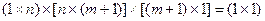т.е. величина скалярная, следовательно, оно не меняется при транспонировании, т.е.

.

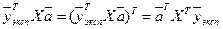Поэтому условие минимизации (2.11) примет вид:

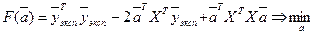. (2.12)

На основании необходимого условия экстремума функции нескольких переменных 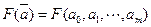необходимо приравнять нулю частные производные по этим переменным или в матричной форме – вектор частных производных

.

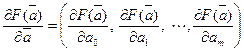Для вектора частных производных в курсе высшей математики доказаны следующие формулы:

,

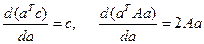где a и c – вектор-столбцы; A – симметричная матрица.

.

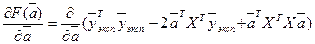Полагая 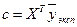, а матрицу 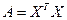(она является симметричной), найдем:

,

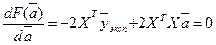откуда получаем систему нормальных уравнений в матричной форме для определения вектора :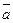

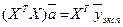. (2.13)

Раскроем последнее выражение

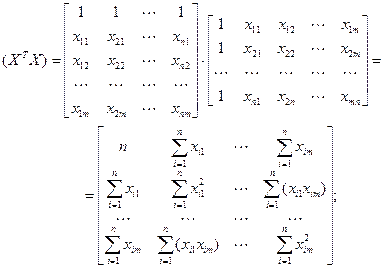(2.14)

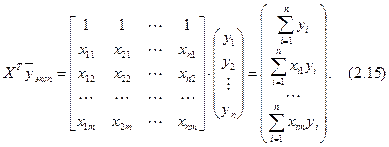
В частном случае из рассматриваемого матричного уравнения (2.13) с учетом (2.14) и (2.15) для одной переменной (m =1) нетрудно получить уже рассмотренную систему нормальных уравнений (2.7). Действительно, в этом случае матричное уравнение (2.13) принимает вид:

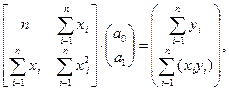
откуда непосредственно следует система нормальных уравнений для парной линейной регрессии.

Умножая слева обе части уравнения (2.13) на обратную матрицу 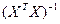определим искомые коэффициенты уравнения регрессии (2.8)

.

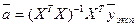Если уравнение регрессии задано в виде полинома степени p

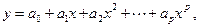
то матрица X называется матрицей Вандермонда и имеет следующую структуру

.

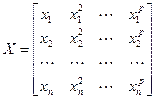Дата добавления: 2014-01-03