Планирование второго порядка

Обычно исследователь начинает изучение объекта или процесса с моделей максимально низкого порядка, т.е. первого. Необходимость перехода к уравнениям второго порядка возникает либо когда есть априорная информация о существенной нелинейности модели (тогда исследование начинают с построения квадратичного уравнения регрессии), либо когда построенная линейная модель оказалась неадекватной (и тогда исследование продолжают, переходя к квадратной модели). Во втором случае желательно использовать максимум информации, извлеченной из линейного плана.

В случае квадратичной модели уже недостаточно варьировать факторы только на двух уровнях. Так, полное уравнение второго порядка для двух факторов

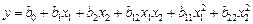
содержит 6 неизвестных коэффициентов регрессии, а варьирование на двух уровнях дает 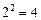точки. В то же время полный факторный эксперимент 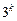явно избыточен.

Существует ряд подходов к построению планов второго порядка, более экономных, чем ПФЭ и, в то же время, отвечающих требованиям оптимальности. Заметим, что, в отличие от линейных планов, в планах второго порядка не удается одновременно обеспечить сочетание всех свойств (ортогональности, ротатабельности и др.).

Один из подходов к построению планов второго порядка основывается на максимально возможном использовании информации, полученной при линейном планировании. Здесь планы второго порядка получают путем добавления 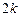точек (где 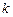— число факторов), называемых «звездными» точками, и точки в центре плана к плану ПФЭ 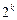или ДФЭ 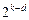. Предполагается, что в центральной точке может ставиться несколько опытов, число которых 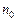зависит от свойств плана.

Тогда общее число опытов для плана второго порядка

,

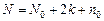где .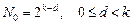

«Звездные» точки выбираются на осях факторного пространства, по две на каждой из осей, на равных расстояниях от центра плана (рис. 3.2). Расстояние 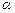от начала координат до «звездной» точки называется «звездным» плечом. Запишем план второго порядка для 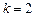и 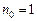(табл. 3.4).

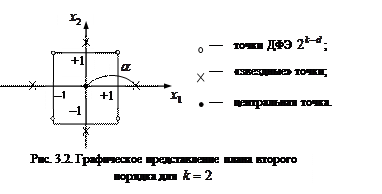Таблица 3.4

План второго порядка для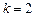

№
	+	–	–	+	+	+
	+	+	–	–	+	+
	+	–	+	–	+	+
	+	+	+	+	+	+
	+
	+
	+
	+

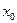
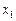
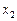
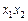
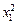
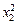
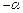
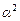
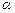
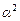
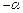
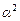
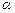
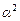
Таким образом, здесь каждый из факторов варьируется на пяти уровнях: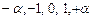. В рассматриваемых планах расположение точек на осях не нарушает ортогональности столбцов первого порядка и эффектов взаимодействия. Это дает возможность получать независимыми соответствующие коэффициенты уравнения регрессии. Но здесь ортогональность плана нарушается для столбцов 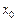и :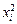

,

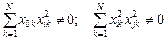так как 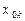всегда равно единице, а неотрицательные величины 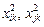не могут быть все равны нулю.

Чтобы получить ортогональное планирование второго порядка, нужно произвести некоторое преобразование квадратичных переменных и оптимальным образом выбрать величину «звездного» плеча.

Дата добавления: 2014-01-03